AutoMathic

The Smart Calculator for Automated Math

(C) 1988, 2024 Kevin B. Belton

Home

Features

Screenshots

Examples

Testimonials

News

Documentation

Support

We've all wondered about something, but never bothered to figure it out because it was "too much trouble".

"I could figure it out...", you say to yourself,

"but it would take too long", or
"I don't remember all the exact formulas", or
"I'd have to convert everything to the right units first".

"Besides", you continue, "it's not that important anyway..."

AutoMathic is intended to raise the bar of what you would consider "too much trouble". The ability to conveniently get answers to mathematical questions frees you to ask more (and more interesting) questions since the program takes away the drudgery of getting answers!

AutoMathic is a flexible and very open-ended tool. Like any tool it will enhance, not replace, your own ability! To get the most out of AutoMathic, especially its "Converse" mode, you have to put some effort into it... The more effort you put into understanding it, what it knows, and what it can do for you, the more you will get out of it! AutoMathic will pay back that effort by allowing you to easily answer those questions that you could probably solve on your own (given time and/or patience), but wouldn't bother to for any number of reasons. If only you could delegate to a smart assistant, leaving yourself more time to focus on more important things...

If you have a mathematical question to answer, you can do it all yourself, or you can let AutoMathic help you do it!

With AutoMathic, you focus on specifying the problem, and let the computer do the mechanical work of solving it!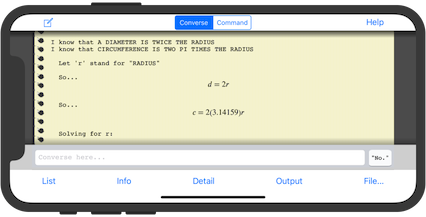

The documentation has lots of examples throughout the main body, in the quick-references, and in the lexicon... The examples were chosen to demonstrate not only AutoMathic's vocabulary, but also a wide range of its grammar and default knowledge. By seeing examples of its language in an understandable context, the user should begin to learn AutoMathic's "dialect" of English in the same way they might learn a foreign language by being immersed in it.

Examples
(Click here for browsers without MathML support)

Here is just a sneak peek at the kinds of things understood by AutoMathic's "Converse" mode. These examples show how it doesn't just calculate... It is smart enough to help you solve problems!

* Except where noted, AutoMathic's output in these examples has been abbreviated to focus on how it:

Understands your raw input, and
Returns meaningful answers.

AutoMathic always generates full step-by-step solutions with as much or little detail as you want!

General Math

Numbers and Numeric Constants
Arithmetic Expressions
Algebraic Equations
Percentages
Money
Circles

Units and Unit Conversion

Simple Units
Compound Units
Multi-dimensional Units

Physics & Chemistry

General Math

Numbers and Numeric Constants:

You enter...	AutoMathic understands...
Two	2
Two pair	4
-0.125	-0.125 (or -1 / 8)
A thousand	1,000
Seven trillion	7,000,000,000,000
Tens	10
100's	100
A sixteenth	0.0625 (or 1 / 16)
A 16th	0.0625 (or 1 / 16)
Two thirds	0.666666666666667 (or 2 / 3)
2 3rds	0.666666666666667 (or 2 / 3)
2/3rds	0.666666666666667 (or 2 / 3)
Four tenths	0.4 (or 2 / 5)
4 10ths	0.4 (or 2 / 5)
8 billionths	0.000000008
8 1,000,000,000ths	0.000000008
Three baker's dozens	39
6 gross	864
Pi	3.14159
Tau	6.28318
e	2.71828
Golden ratio	1.61803
Avogadro's number	602,200,000,000,000,000,000,000

Arithmetic Expressions: (+, -, *, /, plus, minus, times, divided by, etc.)

You enter...	AutoMathic understands...
Three Pi over two	4.712385
Twice the length added to twice the width	$2 l + 2 w$
Twice the sum of the length and the width	$2 (l + w)$
3x the diameter	$3 d$
Half the mass	$\frac{m}{2}$
A third of the sum of cost and tip	$\frac{c + t}{3}$
The ratio of width to height	$\frac{w}{h}$
The cost without half the taxes	$c - \frac{t}{2}$

Algebraic Equations: (=, equals, is, are, was, were, etc.)

You enter...	AutoMathic understands...
Twice the sum of the width and the length is the perimeter.	$2 (l + w) = p$
The area would be half the base times the height.	$a = \frac{b h}{2}$
How much less than e is Pi over two?	$2.71828 - a = \frac{3.14159}{2}$ 1.147485 is THE ANSWER.
Half of what age is three more than a fourth of itself?	$\frac{a}{2} = 3 + \frac{a}{4}$ 12 is THE AGE.

Percentages: (%, percent, pct, percentage, etc.)

You enter...	AutoMathic understands...
12% of 275 million	$\frac{12}{100} 275 (1000000)$ 33,000,000 is 12% OF 275 MILLION.
8.25 percent more than 198	$(1 + \frac{8.25}{100}) 198$ 214.335 is 8.25% MORE THAN 198.
12 pct less than 224.99	$224.99 (1 - \frac{3}{25})$ 197.9912 is 12% LESS THAN 224.99.
5% of each donation is overhead	$\frac{5}{100} d = o$
How many millions is 12% of 275 million?	$1000000 n = 33000000$ 33 is THE NUMBER.
What percentage of fifty is thirty?	$\frac{p}{100} (50) = 30$ 60 is THE PERCENTAGE.
Two dozen makes up only 20% of what total?	$12 (2) = \frac{20}{100} t$ $24 = \frac{t}{5}$ 120 is THE TOTAL.
What percent is one seventh?	$\frac{a}{100} = \frac{1}{7}$ 14.2857142857143 (or 100 / 7, or 14 & 2 / 7) is THE ANSWER.
Seventy percent is the ratio of successes to attempts.	$\frac{70}{100} = \frac{s}{a}$
Thirty is a dozen less than 97% of what age?	$30 = \frac{97 a}{100} - 12$ 43.298969072165 is THE AGE.

Money: (price, tax, cost, tip)

You enter...	AutoMathic understands...
What percentage of a cost are its taxes?	(Find p) $\frac{c p}{100} = t$ 7.62124711316397 is THE PERCENTAGE.
What must the price have been assuming that tips were 2.75?	(Find p) $t = 2.75$ 16.9361046959199 is THE PRICE.
The price is 12% off of what when the cost is 225?	(Find a) $p = (1 - \frac{3}{25}) a$ $c = 225$ 236.195674994751 is THE AMOUNT.
The price consists of 0.65 per apple and 1.25 per drink.	$p = 0.65 a + 1.25 d$
The price for each tire is 79.95. Find the cost for 5 tires.	$\frac{p}{t} = 79.95$ (Find 5c/t) 432.729375 is THE COST FOR 5 TIRES.
Find the price such that the cost is 225.	(Find p) $c = 225$ 207.852193995381 is THE PRICE.

Circles: (radius, diameter, circumference)

You enter...	AutoMathic understands...
The circumference is how many times the radius?	$c = n r$ $c = 2 (3.14159) r$ 6.28318 is THE NUMBER.
21 is the difference between what circumference and what radius?	(Find r) (Find c) $21 = c - r$ $c = 2 (3.14159) r$ 24.9748787661976 is THE CIRCUMFERENCE. 3.97487876619763 is THE RADIUS.
Compute the circumference where the diameter is 13.	(Find c) $d = 13$ $d = 2 r$ $c = 2 (3.14159) r$ 40.84067 is THE CIRCUMFERENCE.
When the radius is 3, how much more than that's the circumference?	$r = 3$ (Find a) $a + r = c$ $c = 2 (3.14159) r$ 15.84954 is THE ANSWER.

Units and Unit Conversion

Simple Units:

Category	Built-in Units (not including abbreviations)
Length	millimeters, centimeters, inches, feet, meters, yards, fathoms, furlongs, kilometers, miles, nautical miles, leagues, microns / micrometers, nanometers, angstroms, astronomical units, light years, parsecs
Time	nanoseconds, microseconds, milliseconds, seconds, minutes, hours, days, weeks, fortnights, months, years, decades, centuries, millenia
Weight & Mass	ounces, pounds, tons, milligrams, grams, kilograms, AMU, metric tons, kilotons
Liquid / Volume	teaspoons, tablespoons, fluid ounces, cups, pints, quarts, gallons, milliliters, liters, drops
Temperature	Fahrenheit, Celsius / Centigrade, Kelvin
Pressure	atmospheres, psi, torr, inches of mercury, millimeters of mercury, pascals, kilopascals, bars, millibars
Frequency	hertz, kilohertz, megahertz, gigahertz
Clock & Calendar Frequency	hourly, daily, weekly, monthly, quarterly, yearly, etc.
Angular	radians, degrees, gradians, grads, right angles, revolutions, rotations, circles, arcminutes, arcseconds
Information Storage	bits, nibbles, bytes, words, longwords, kilobytes, megabytes, gigabytes, terabytes, petabytes, kilobits, megabits, gigabits
Electrical	amperes, milliamperes, coulombs, volts, farads, microfarads, picofarads

You enter...	AutoMathic understands...
Inches per meter?	(Find i/m) 39.3700787401575 is INCHES PER METER.
Seconds in 1.5 hrs	(Find 1.5s/h) 5,400 is SECONDS IN 1.5 HRS.
What's 165[lb] in terms of [kg's]?	(Find 165k/p) 75 is 165 [LB] IN TERMS OF [KG'S].
How many unit cc's is 5 unit pints?	$\frac{n}{m} = \frac{5}{p}$ 2,365.625 is THE NUMBER.
The temperature measured in degrees F is 78. What's the temperature in terms of Kelvin?	$f t = 78$ (Find kt) 298.715555555556 is THE TEMPERATURE IN TERMS OF KELVIN.
Convert 90[PSI] into [mmHg].	(Find 90t/p) 4,653.0612244898 is CONVERT 90 [PSI] INTO [MMHG].
How many times 2.4[mHz] is 3.1[gHz]?	$\frac{2.4 n}{m} = \frac{3.1}{g}$ 1,291.66666666667 is THE NUMBER.
Find the cost daily when the cost semiannually is 475.	(Find c/d) $\frac{c}{s} = 475$ 2.6009582477755 is THE COST DAILY.
How many [deg's] is 1.5 pi [radians]?	$\frac{n}{d} = \frac{1.5 (3.14159)}{r}$ 270 is THE NUMBER.
What percentage of 54[mb] is 24[kb]?	$\frac{27 p}{50 m} = \frac{24}{k}$ 0.0434027777777778 (or 25 / 576) is THE PERCENTAGE.

Compound Units:

Category	Component Units	Built-in Units and Constants (including some abbreviations)
Speed	length / time	miles per hour (MPH), kilometers per hour (KPH), feet per second (FPS), meters per second (MPS), knots, speed of sound (mach _), speed of light (_ C)
Angular Velocity	angle / time	revolutions per minute (RPM)
Acceleration	speed / time	G's, Gees, G forces, etc.
Momentum	mass x speed
Force	mass x acceleration	newtons (N)
Density	mass / volume	density of water, mercury, alcohol, gasoline, air, helium, carbon dioxide, steam, aluminum, iron, steel, copper, lead, gold
Concentration	number / volume	moles per liter (_ molar)
Energy, Work, Torque	force x length	joules (J), kilojoules (kJ), calories (cal), food calories / kilocalories (kcal), watt hours (Wh), kilowatt hours (kWh), British thermal units (BTUs)
Power	energy / time	watts (W), kilowatts (kW), horsepower (HP)
Specific Heat	energy / mass	specific heat of water, ice, steam, mercury, alcohol, aluminum, copper, glass, iron, steel, lead, wood, flesh
Fuel Efficiency	length / volume	miles per gallon (MPG)
Bandwidth	storage / time

You enter...	AutoMathic understands...
The speed is 65[mph]. How many [kph] is a third of the speed?	$s = \frac{65 h}{m}$ $\frac{n h}{k} = \frac{s}{3}$ 34.86912 is THE NUMBER.
What's 55[mph] in terms of [furlongs/fortnight]?	(Find 55fh/(mF)) 147,840 is 55 [MPH] IN TERMS OF [FURLONGS/FORTNIGHT].
3[drops/sec] converts to how many [gallons/day]?	$\frac{3 s}{d} = \frac{n D}{g}$ 3.42404227212682 is THE NUMBER.
Convert 1.3[gm/cc] into [lb/gal].	(Find 1.3mp/(gG)) 10.8251 is CONVERT 1.3 [GM/CC] INTO [LB/GAL].
How many times 5[km/l] is 23[mpg]?	$\frac{5 l n}{k} = \frac{23 g}{m}$ 1.95587381770145 is THE NUMBER.
How many unit MB'S is 196[kilobits/sec] x 3.5[min]?	$\frac{n}{m} = \frac{686 s}{M k}$ 4.90665435791016 is THE NUMBER.
There are 42 gallons a barrel. How many [gallons/sec] does 35,000[barrels/day] convert to?	$42 = \frac{g}{b}$ $\frac{n s}{g} = \frac{35000 d}{b}$ 17.0138888888889 is THE NUMBER.

Multi-dimensional Units:

Category	Component Units	Built-in Units (including some abbreviations)
Area	length₁ x length₂ length squared length sqrd length sqr length sq length ^ 2	acres (ac), sections, hectares (ha)
Area	length2	inch2 (in2), foot2 (ft2), yard2 (yd2), mile2 (mi2), nautical mile2 (nmi2) inches2 (ins2), feet2 (ft2), yards2 (yds2), miles2 (mis2), nautical miles2 (nmis2) millimeter2 (mm2), centimeter2 (cm2), meter2 (m2), kilometer2 (km2) millimeters2 (mms2), centimeters2 (cms2), meters2 (ms2), kilometers2 (kms2)
Area	square length squared length sq length sqr length sqrd length	square inch, square foot, square yard, square mile, square nautical mile square inches, square feet, square yards, square miles, square nautical miles square millimeter, square centimeter, square meter, square kilometer square millimeters, square centimeters, square meters, square kilometers sq in, sq ft, sq yd, sq mi, sq nmi sq ins, sq ft, sq yds, sq mis, sq nmis sq mm, sq cm, sq m, sq km sq mms, sq cms, sq ms, sq kms
Volume	length₁ x length₂ x length₃ length cubed length cbd length ^ 3	teaspoons, tablespoons, fluid ounces, cups, pints, quarts, gallons, milliliters, liters, drops
Volume	length3	inch3 (in3), foot3 (ft3), yard3 (yd3), mile3 (mi3), nautical mile3 (nmi3) inches3 (ins3), feet3 (ft3), yards3 (yds3), miles3 (mis3), nautical miles3 (nmis3) millimeter3 (mm3), centimeter3 (cm3), meter3 (m3), kilometer3 (km3) millimeters3 (mms3), centimeters3 (cms3), meters3 (ms3), kilometers3 (kms3)
Volume	cubic length cubed length cu length cbd length	cubic inch, cubic foot, cubic yard, cubic mile, cubic nautical mile cubic inches, cubic feet, cubic yards, cubic miles, cubic nautical miles cubic millimeter, cubic centimeter, cubic meter, cubic kilometer cubic millimeters, cubic centimeters, cubic meters, cubic kilometers cu in, cu ft, cu yd, cu mi, cu nmi cu ins, cu ft, cu yds, cu mis, cu nmis cu mm, cu cm, cu m, cu km cu mms, cu cms, cu ms, cu kms
Time²	time₁ x time₂ time squared time sqrd time sqr time sq time ^ 2
Time²	time2	second2 (sec2, s2), seconds2 (secs2)
Time³	time₁ x time₂ x time₃ time cubed time cbd time ^ 3
Time³	time3	second3 (sec3, s3), seconds3 (secs3)
Other²	unit₁ x unit₂ unit squared unit sqrd unit sqr unit sq unit ^ 2
Other³	unit₁ x unit₂ x unit₃ unit cubed unit cbd unit ^ 3
Other^N	unit₁ x unit₂ x ... x unit_N

You enter...	AutoMathic understands...
If the area is 5x7[in^2], what's the area in [cm2]?	$a = \frac{35}{i i}$ (Find acc) 225.806 is THE AREA IN [CM2].
What's 350[in cubed] in terms of [cm^3]? What's 350[in cubed] measured in gallons?	(Find 350ccc/(iii)) (Find 350g/(iii)) 5,735.4724 is 350 [IN CUBED] IN TERMS OF [CM^3]. 1.51531635402906 is 350 [IN CUBED] MEASURED IN GALLONS.
Convert 8[ft] by 3[ft] by 7[ft] into [meters^3].	(Find 168mmm/(fff)) 4.757230227456 is CONVERT 8 [FT] BY 3 [FT] BY 7 [FT] INTO [METERS^3].
3,000[ft squared] is 40[ft] times how many unit yards?	$\frac{3000}{f f} = \frac{40 n}{f y}$ $\frac{3000}{f} = \frac{40 n}{y}$ 25 is THE NUMBER.
How many [ft sq] is 2x6[m^2]?	$\frac{n}{f f} = \frac{12}{m m}$ 129.1669250000517 is THE NUMBER.
What percentage of 1[meter cubed] is 4[in] x 6[in] x 8[in]?	$\frac{p}{100 m m m} = \frac{192}{i i i}$ 0.3146316288 is THE PERCENTAGE.
How many times 2[ft cubed] is 2[in] x 1[m] x 25[ft]?	$\frac{2 n}{f f f} = \frac{50}{f i m}$ $\frac{2 n}{f f} = \frac{50}{i m}$ 6.83508311461067 is THE NUMBER.
How many [feet/(second^2)] is 5.5 Gee?	$\frac{n s s}{f} = \frac{5.5 (9.8) s s}{m}$ $\frac{n}{f} = \frac{5.5 (9.8)}{m}$ 176.837270341207 is THE NUMBER.

Physics & Chemistry

Average Speed: (distance, average speed or constant speed, time)

You enter...

If the average speed is 130[mph], and the time is 73[sec], find the distance measured in kilometers.

AutoMathic understands...

Let 'a' stand for "AVERAGE SPEED"

Let 'm' stand for "MILE"

Let 'h' stand for "HOUR"

So...
 $a = \frac{130 h}{m}$ 

Let 't' stand for "TIME"

Let 's' stand for "SECOND"

So...
 $t = \frac{73}{s}$ 

Let 'd' stand for "DISTANCE"

Let 'k' stand for "KILOMETERS"

(Find dk)

Anything else?

> No.

I know that THERE ARE A HUNDRED CENTIMETERS IN A METER
I know that THERE ARE 2.54 CENTIMETERS PER INCH
I know that THERE ARE TWELVE INCHES IN A FOOT
I know that THERE ARE 5280 FEET IN A MILE
I know that THERE ARE A THOUSAND METERS IN A KILOMETER
I know that THERE ARE SIXTY SECONDS IN A MINUTE
I know that THERE ARE SIXTY MINUTES IN AN HOUR
I know that DISTANCE IS AVERAGE SPEED TIMES TIME
I know that ACCELERATION IS SPEED OVER TIME
I know that DISTANCE IS ONE HALF SPEED TIMES TIME

Let 'c' stand for "CENTIMETERS"

Let 'M' stand for "METER"

So...
 $100 = \frac{c}{M}$ 

Let 'i' stand for "INCH"

So...
 $2.54 = \frac{c}{i}$ 

Let 'f' stand for "FOOT"

So...
 $12 = \frac{i}{f}$ 

So...
 $5280 = \frac{f}{m}$ 

So...
 $1000 = \frac{M}{k}$ 

Let 'I' stand for "MINUTE"

So...
 $60 = \frac{s}{I}$ 

So...
 $60 = \frac{I}{h}$ 

So...
 $d = a t$ 

Let 'A' stand for "ACCELERATION"

Let 'S' stand for "SPEED"

So...
 $A = \frac{S}{t}$ 

So...
 $d = \frac{S t}{2}$ 

Hypothetically...

m = 1

Solving for f:

 $\begin{matrix} 5280 & = & \frac{f}{m} \\ \frac{f}{m} & = & 5280 \\ f \frac{1}{m} & = & 5280 \\ f & = & 5280 m \end{matrix}$ 
 f = 5,280

Solving for i:

 $\begin{matrix} 12 & = & \frac{i}{f} \\ \frac{i}{f} & = & 12 \\ i \frac{1}{f} & = & 12 \\ i & = & 12 f \end{matrix}$ 
 i = 63,360

Solving for c:

 $\begin{matrix} 2.54 & = & \frac{c}{i} \\ \frac{c}{i} & = & 2.54 \\ c \frac{1}{i} & = & 2.54 \\ c & = & 2.54 i \end{matrix}$ 
 c = 160,934.4

Solving for M:

 $\begin{matrix} 100 & = & \frac{c}{M} \\ \frac{c}{M} & = & 100 \\ c & = & 100 M \\ 100 M & = & c \\ M (100) & = & c \\ M & = & \frac{c}{100} \end{matrix}$ 
 M = 1,609.344

Solving for k:

 $\begin{matrix} 1000 & = & \frac{M}{k} \\ \frac{M}{k} & = & 1000 \\ M & = & 1000 k \\ 1000 k & = & M \\ k (1000) & = & M \\ k & = & \frac{M}{1000} \end{matrix}$ 
 k = 1.609344

Hypothetically...

I = 1

Solving for s:

 $\begin{matrix} 60 & = & \frac{s}{I} \\ \frac{s}{I} & = & 60 \\ s \frac{1}{I} & = & 60 \\ s & = & 60 I \end{matrix}$ 
 s = 60

Solving for h:

 $\begin{matrix} 60 & = & \frac{I}{h} \\ \frac{I}{h} & = & 60 \\ I & = & 60 h \\ 60 h & = & I \\ h (60) & = & I \\ h & = & \frac{I}{60} \end{matrix}$ 
 h = 0.0166666666666667 (or 1 / 60)

 $a = \frac{130 h}{m}$ 
 a = 2.16666666666667 (or 13 / 6, or 2 & 1 / 6)

 $t = \frac{73}{s}$ 
 t = 1.21666666666667 (or 73 / 60, or 1 & 13 / 60)

 $d = a t$ 
 d = 2.63611111111111 (or 949 / 360, or 2 & 229 / 360)

Solving for S:

 $\begin{matrix} d & = & \frac{S t}{2} \\ \frac{S t}{2} & = & d \\ S \frac{t}{2} & = & d \\ S t & = & 2 d \\ S t & = & 2 d \\ S & = & \frac{2 d}{t} \end{matrix}$ 
 S = 4.33333333333333 (or 13 / 3, or 4 & 1 / 3)

 $A = \frac{S}{t}$ 
 A = 3.56164383561644 (or 260 / 73, or 3 & 41 / 73)

4.2424096 is THE DISTANCE MEASURED IN KILOMETERS.

Acceleration: (acceleration, speed (or velocity, instantaneous speed, variable speed, or changing speed), time)

You enter...

How many Gees is the acceleration if the speed was 60[mph], and the time was 3.4[sec]?

AutoMathic understands...

Let 'n' stand for "NUMBER"

(Find n)

Let 'm' stand for "METERS"

Let 's' stand for "SECOND"

Let 'a' stand for "ACCELERATION"

So...
 $\frac{9.8 n s s}{m} = a$ 

Let 'S' stand for "SPEED"

Let 'M' stand for "MILE"

Let 'h' stand for "HOUR"

So...
 $S = \frac{60 h}{M}$ 

Let 't' stand for "TIME"

So...
 $t = \frac{3.4}{s}$ 

Anything else?

> No.

I know that THERE ARE A HUNDRED CENTIMETERS IN A METER
I know that THERE ARE 2.54 CENTIMETERS PER INCH
I know that THERE ARE TWELVE INCHES IN A FOOT
I know that THERE ARE 5280 FEET IN A MILE
I know that THERE ARE SIXTY SECONDS IN A MINUTE
I know that THERE ARE SIXTY MINUTES IN AN HOUR
I know that DISTANCE IS AVERAGE SPEED TIMES TIME
I know that ACCELERATION IS SPEED OVER TIME
I know that DISTANCE IS ONE HALF SPEED TIMES TIME

Let 'c' stand for "CENTIMETERS"

So...
 $100 = \frac{c}{m}$ 

Let 'i' stand for "INCH"

So...
 $2.54 = \frac{c}{i}$ 

Let 'f' stand for "FOOT"

So...
 $12 = \frac{i}{f}$ 

So...
 $5280 = \frac{f}{M}$ 

Let 'I' stand for "MINUTE"

So...
 $60 = \frac{s}{I}$ 

So...
 $60 = \frac{I}{h}$ 

Let 'd' stand for "DISTANCE"

Let 'A' stand for "AVERAGE SPEED"

So...
 $d = A t$ 

So...
 $a = \frac{S}{t}$ 

So...
 $d = \frac{S t}{2}$ 

Hypothetically...

m = 1

Solving for c:

 $\begin{matrix} 100 & = & \frac{c}{m} \\ \frac{c}{m} & = & 100 \\ c \frac{1}{m} & = & 100 \\ c & = & 100 m \end{matrix}$ 
 c = 100

Solving for i:

 $\begin{matrix} 2.54 & = & \frac{c}{i} \\ \frac{c}{i} & = & 2.54 \\ c & = & 2.54 i \\ 2.54 i & = & c \\ i (2.54) & = & c \\ i & = & \frac{c}{2.54} \end{matrix}$ 
 i = 39.3700787401575

Solving for f:

 $\begin{matrix} 12 & = & \frac{i}{f} \\ \frac{i}{f} & = & 12 \\ i & = & 12 f \\ 12 f & = & i \\ f (12) & = & i \\ f & = & \frac{i}{12} \end{matrix}$ 
 f = 3.28083989501312

Solving for M:

 $\begin{matrix} 5280 & = & \frac{f}{M} \\ \frac{f}{M} & = & 5280 \\ f & = & 5280 M \\ 5280 M & = & f \\ M (5280) & = & f \\ M & = & \frac{f}{5280} \end{matrix}$ 
 M = 0.000621371192237334

Hypothetically...

s = 1

 $t = \frac{3.4}{s}$ 
 t = 3.4 (or 17 / 5, or 3 & 2 / 5)

Solving for I:

 $\begin{matrix} 60 & = & \frac{s}{I} \\ \frac{s}{I} & = & 60 \\ s & = & 60 I \\ 60 I & = & s \\ I (60) & = & s \\ I & = & \frac{s}{60} \end{matrix}$ 
 I = 0.0166666666666667 (or 1 / 60)

Solving for h:

 $\begin{matrix} 60 & = & \frac{I}{h} \\ \frac{I}{h} & = & 60 \\ I & = & 60 h \\ 60 h & = & I \\ h (60) & = & I \\ h & = & \frac{I}{60} \end{matrix}$ 
 h = 0.000277777777777778

 $S = \frac{60 h}{M}$ 
 S = 26.8224

 $a = \frac{S}{t}$ 
 a = 7.88894117647059

 $d = \frac{S t}{2}$ 
 d = 45.59808

Solving for n:

 $\begin{matrix} \frac{9.8 n s s}{m} & = & a \\ n \frac{9.8 s s}{m} & = & a \\ 9.8 n s s & = & a m \\ n (9.8 s s) & = & a m \\ n & = & \frac{a m}{9.8 s s} \end{matrix}$ 
 n = 0.80499399759904

Solving for A:

 $\begin{matrix} d & = & A t \\ A t & = & d \\ A t & = & d \\ A & = & \frac{d}{t} \end{matrix}$ 
 A = 13.4112

0.80499399759904 is THE NUMBER.

Uniformly Accelerated Motion: (speed (or velocity, instantaneous speed, variable speed, or changing speed), time, distance)

You enter...

Given that the distance is a quarter of a unit mile, and the time is 5.6[sec], find the speed measured in mph.

AutoMathic understands...

Let 'd' stand for "DISTANCE"

Let 'm' stand for "MILE"

So...
 $d = \frac{1}{4 m}$ 

Let 't' stand for "TIME"

Let 's' stand for "SECOND"

So...
 $t = \frac{5.6}{s}$ 

Let 'S' stand for "SPEED"

Let 'h' stand for "HOUR"

(Find Sm/h)

Anything else?

> No.

I know that THERE ARE SIXTY SECONDS IN A MINUTE
I know that THERE ARE SIXTY MINUTES IN AN HOUR
I know that DISTANCE IS AVERAGE SPEED TIMES TIME
I know that ACCELERATION IS SPEED OVER TIME
I know that DISTANCE IS ONE HALF SPEED TIMES TIME

Let 'M' stand for "MINUTE"

So...
 $60 = \frac{s}{M}$ 

So...
 $60 = \frac{M}{h}$ 

Let 'a' stand for "AVERAGE SPEED"

So...
 $d = a t$ 

Let 'A' stand for "ACCELERATION"

So...
 $A = \frac{S}{t}$ 

So...
 $d = \frac{S t}{2}$ 

Hypothetically...

h = 1

Solving for M:

 $\begin{matrix} 60 & = & \frac{M}{h} \\ \frac{M}{h} & = & 60 \\ M \frac{1}{h} & = & 60 \\ M & = & 60 h \end{matrix}$ 
 M = 60

Solving for s:

 $\begin{matrix} 60 & = & \frac{s}{M} \\ \frac{s}{M} & = & 60 \\ s \frac{1}{M} & = & 60 \\ s & = & 60 M \end{matrix}$ 
 s = 3,600

 $t = \frac{5.6}{s}$ 
 t = 0.00155555555555556

(Setting the free variable 'd' to 1)

d = 1

Solving for m:

 $\begin{matrix} d & = & \frac{1}{4 m} \\ \frac{1}{4 m} & = & d \\ 1 & = & 4 d m \\ 4 d m & = & 1 \\ m (4 d) & = & 1 \\ m & = & \frac{1}{4 d} \end{matrix}$ 
 m = 0.25 (or 1 / 4)

Solving for a:

 $\begin{matrix} d & = & a t \\ a t & = & d \\ a t & = & d \\ a & = & \frac{d}{t} \end{matrix}$ 
 a = 642.857142857143

Solving for S:

 $\begin{matrix} d & = & \frac{S t}{2} \\ \frac{S t}{2} & = & d \\ S \frac{t}{2} & = & d \\ S t & = & 2 d \\ S t & = & 2 d \\ S & = & \frac{2 d}{t} \end{matrix}$ 
 S = 1,285.71428571429

 $A = \frac{S}{t}$ 
 A = 826,530.612244898

321.428571428571 is THE SPEED MEASURED IN MPH.

Force: (force, mass, acceleration)

You enter...

Find the mass measured in lbs so that the force is 750[N] when acceleration is 1 Gee.

AutoMathic understands...

Let 'm' stand for "MASS"

Let 'p' stand for "POUND"

(Find mp)

Let 'f' stand for "FORCE"

Let 'k' stand for "KILOGRAM"

Let 'M' stand for "METERS"

Let 's' stand for "SECOND"

So...
 $f = \frac{750 s s}{M k}$ 

Let 'a' stand for "ACCELERATION"

So...
 $a = \frac{9.8 s s}{M}$ 

Anything else?

> No.

I know that THERE ARE 2.2 POUNDS IN A KILOGRAM
I know that FORCE IS MASS TIMES ACCELERATION

So...
 $2.2 = \frac{p}{k}$ 

So...
 $f = a m$ 

Hypothetically...

M = 1

Hypothetically...

s = 1

 $a = \frac{9.8 s s}{M}$ 
 a = 9.8 (or 49 / 5, or 9 & 4 / 5)

Hypothetically...

k = 1

 $f = \frac{750 s s}{M k}$ 
 f = 750

Solving for p:

 $\begin{matrix} 2.2 & = & \frac{p}{k} \\ \frac{p}{k} & = & 2.2 \\ p \frac{1}{k} & = & 2.2 \\ p & = & 2.2 k \end{matrix}$ 
 p = 2.2 (or 11 / 5, or 2 & 1 / 5)

Solving for m:

 $\begin{matrix} f & = & a m \\ a m & = & f \\ m a & = & f \\ m & = & \frac{f}{a} \end{matrix}$ 
 m = 76.530612244898

168.367346938776 is THE MASS MEASURED IN LBS.

Centripetal Acceleration: (centripetal acceleration or centrifugal acceleration, average speed or constant speed, radius)

You enter...

If the average speed is 50[kph], and the radius is 50[m], how many G's would the centripetal acceleration be?

AutoMathic understands...

Let 'a' stand for "AVERAGE SPEED"

Let 'k' stand for "KILOMETER"

Let 'h' stand for "HOUR"

So...
 $a = \frac{50 h}{k}$ 

Let 'r' stand for "RADIUS"

Let 'm' stand for "METER"

So...
 $r = \frac{50}{m}$ 

Let 'n' stand for "NUMBER"

(Find n)

Let 's' stand for "SECOND"

Let 'c' stand for "CENTRIPETAL ACCELERATION"

So...
 $\frac{9.8 n s s}{m} = c$ 

Anything else?

> No.

I know that THERE ARE A THOUSAND METERS IN A KILOMETER
I know that THERE ARE SIXTY SECONDS IN A MINUTE
I know that THERE ARE SIXTY MINUTES IN AN HOUR
I know that CENTRIPETAL ACCELERATION IS AVERAGE SPEED TIMES ITSELF OVER RADIUS

So...
 $1000 = \frac{m}{k}$ 

Let 'M' stand for "MINUTE"

So...
 $60 = \frac{s}{M}$ 

So...
 $60 = \frac{M}{h}$ 

So...
 $c = \frac{a a}{r}$ 

Hypothetically...

k = 1

Solving for m:

 $\begin{matrix} 1000 & = & \frac{m}{k} \\ \frac{m}{k} & = & 1000 \\ m \frac{1}{k} & = & 1000 \\ m & = & 1000 k \end{matrix}$ 
 m = 1,000

 $r = \frac{50}{m}$ 
 r = 0.05 (or 1 / 20)

Hypothetically...

s = 1

Solving for M:

 $\begin{matrix} 60 & = & \frac{s}{M} \\ \frac{s}{M} & = & 60 \\ s & = & 60 M \\ 60 M & = & s \\ M (60) & = & s \\ M & = & \frac{s}{60} \end{matrix}$ 
 M = 0.0166666666666667 (or 1 / 60)

Solving for h:

 $\begin{matrix} 60 & = & \frac{M}{h} \\ \frac{M}{h} & = & 60 \\ M & = & 60 h \\ 60 h & = & M \\ h (60) & = & M \\ h & = & \frac{M}{60} \end{matrix}$ 
 h = 0.000277777777777778

 $a = \frac{50 h}{k}$ 
 a = 0.0138888888888889 (or 1 / 72)

 $c = \frac{a a}{r}$ 
 c = 0.00385802469135802

Solving for n:

 $\begin{matrix} \frac{9.8 n s s}{m} & = & c \\ n \frac{9.8 s s}{m} & = & c \\ 9.8 n s s & = & c m \\ n (9.8 s s) & = & c m \\ n & = & \frac{c m}{9.8 s s} \end{matrix}$ 
 n = 0.393675988914084

0.393675988914084 is THE NUMBER.

Work: (work, force, distance)

You enter...

How many unit Joules is the work when the mass is 15[kg], acceleration is 1 G, and distance is 12[m]?

AutoMathic understands...

Let 'n' stand for "NUMBER"

(Find n)

Let 'k' stand for "KILOGRAM"

Let 'm' stand for "METERS"

Let 's' stand for "SECOND"

Let 'w' stand for "WORK"

So...
 $\frac{n s s}{k m m} = w$ 

Let 'M' stand for "MASS"

So...
 $M = \frac{15}{k}$ 

Let 'a' stand for "ACCELERATION"

So...
 $a = \frac{9.8 s s}{m}$ 

Let 'd' stand for "DISTANCE"

So...
 $d = \frac{12}{m}$ 

Anything else?

> No.

I know that CIRCUMFERENCE IS TWO PI TIMES THE RADIUS
I know that CIRCUMFERENCE TIMES REVOLUTIONS IS DISTANCE
I know that DISTANCE IS AVERAGE SPEED TIMES TIME
I know that ACCELERATION IS SPEED OVER TIME
I know that DISTANCE IS ONE HALF SPEED TIMES TIME
I know that FORCE IS MASS TIMES ACCELERATION
I know that CENTRIPETAL ACCELERATION IS AVERAGE SPEED TIMES ITSELF OVER RADIUS
I know that WORK IS FORCE TIMES DISTANCE
I know that TORQUE IS FORCE TIMES RADIUS

Let 'c' stand for "CIRCUMFERENCE"

Let 'r' stand for "RADIUS"

So...
 $c = 2 (3.14159) r$ 

Let 'R' stand for "REVOLUTIONS"

So...
 $R c = d$ 

Let 'A' stand for "AVERAGE SPEED"

Let 't' stand for "TIME"

So...
 $d = A t$ 

Let 'S' stand for "SPEED"

So...
 $a = \frac{S}{t}$ 

So...
 $d = \frac{S t}{2}$ 

Let 'f' stand for "FORCE"

So...
 $f = M a$ 

Let 'C' stand for "CENTRIPETAL ACCELERATION"

So...
 $C = \frac{A A}{r}$ 

So...
 $w = d f$ 

Let 'T' stand for "TORQUE"

So...
 $T = f r$ 

(Setting the free variable 's' to 1)

s = 1

(Setting the free variable 'k' to 1)

k = 1

 $M = \frac{15}{k}$ 
 M = 15

(Setting the free variable 'm' to 1)

m = 1

 $a = \frac{9.8 s s}{m}$ 
 a = 9.8 (or 49 / 5, or 9 & 4 / 5)

 $d = \frac{12}{m}$ 
 d = 12

 $f = M a$ 
 f = 147

 $w = d f$ 
 w = 1,764

Solving for n:

 $\begin{matrix} \frac{n s s}{k m m} & = & w \\ n \frac{s s}{k m m} & = & w \\ n s s & = & k m m w \\ n (s s) & = & k m m w \\ n & = & \frac{k m m w}{s s} \end{matrix}$ 
 n = 1,764

1,764 is THE NUMBER.

Kinetic Energy: (kinetic energy (KE), mass, average speed or constant speed)

You enter...

How many unit Joules is the KE given that the average speed is 8.9[m/s], and the mass is 70[kg]?

AutoMathic understands...

Let 'n' stand for "NUMBER"

(Find n)

Let 'k' stand for "KILOGRAM"

Let 'm' stand for "METERS"

Let 's' stand for "SECOND"

Let 'K' stand for "KINETIC ENERGY"

So...
 $\frac{n s s}{k m m} = K$ 

Let 'a' stand for "AVERAGE SPEED"

So...
 $a = \frac{8.9 s}{m}$ 

Let 'M' stand for "MASS"

So...
 $M = \frac{70}{k}$ 

Anything else?

> No.

I know that KINETIC ENERGY IS HALF MASS TIMES AVERAGE SPEED TIMES ITSELF

So...
 $K = \frac{M a a}{2}$ 

Hypothetically...

m = 1

(Setting the free variable 's' to 1)

s = 1

 $a = \frac{8.9 s}{m}$ 
 a = 8.9 (or 89 / 10, or 8 & 9 / 10)

(Setting the free variable 'k' to 1)

k = 1

 $M = \frac{70}{k}$ 
 M = 70

 $K = \frac{M a a}{2}$ 
 K = 2,772.35

Solving for n:

 $\begin{matrix} \frac{n s s}{k m m} & = & K \\ n \frac{s s}{k m m} & = & K \\ n s s & = & K k m m \\ n (s s) & = & K k m m \\ n & = & \frac{K k m m}{s s} \end{matrix}$ 
 n = 2,772.35

2,772.35 is THE NUMBER.

Potential Energy: (potential energy (PE), mass, height)

You enter...

If the mass is 2,200[lb], and the height is 25[m], how many unit kJ's is the potential energy?

AutoMathic understands...

Let 'm' stand for "MASS"

Let 'p' stand for "POUND"

So...
 $m = \frac{2200}{p}$ 

Let 'h' stand for "HEIGHT"

Let 'M' stand for "METER"

So...
 $h = \frac{25}{M}$ 

Let 'n' stand for "NUMBER"

(Find n)

Let 'k' stand for "KILOGRAM"

Let 's' stand for "SECOND"

Let 'P' stand for "POTENTIAL ENERGY"

So...
 $\frac{1000 n s s}{M M k} = P$ 

Anything else?

> No.

I know that THERE ARE 2.2 POUNDS IN A KILOGRAM
I know that POTENTIAL ENERGY IS MASS TIMES 1 G TIMES HEIGHT

So...
 $2.2 = \frac{p}{k}$ 

So...
 $P = \frac{9.8 h m s s}{M}$ 

Hypothetically...

k = 1

Solving for p:

 $\begin{matrix} 2.2 & = & \frac{p}{k} \\ \frac{p}{k} & = & 2.2 \\ p \frac{1}{k} & = & 2.2 \\ p & = & 2.2 k \end{matrix}$ 
 p = 2.2 (or 11 / 5, or 2 & 1 / 5)

 $m = \frac{2200}{p}$ 
 m = 1,000

Hypothetically...

M = 1

 $h = \frac{25}{M}$ 
 h = 25

Hypothetically...

s = 1

 $P = \frac{9.8 h m s s}{M}$ 
 P = 245,000

Solving for n:

 $\begin{matrix} \frac{1000 n s s}{M M k} & = & P \\ n \frac{1000 s s}{M M k} & = & P \\ 1000 n s s & = & M M P k \\ n (1000 s s) & = & M M P k \\ n & = & \frac{M M P k}{1000 s s} \end{matrix}$ 
 n = 245

245 is THE NUMBER.

Power: (power, energy, time)

You enter...

How many unit kW would the power be assuming the energy is potential energy, mass is 160[lb], height was 4.5[m], and the time was 4[sec]?

AutoMathic understands...

Let 'n' stand for "NUMBER"

(Find n)

Let 'k' stand for "KILOGRAM"

Let 'm' stand for "METERS"

Let 's' stand for "SECOND"

Let 'p' stand for "POWER"

So...
 $\frac{1000 n s s s}{k m m} = p$ 

Let 'e' stand for "ENERGY"

Let 'P' stand for "POTENTIAL ENERGY"

So...
 $e = P$ 

Let 'M' stand for "MASS"

Let 'o' stand for "POUND"

So...
 $M = \frac{160}{o}$ 

Let 'h' stand for "HEIGHT"

So...
 $h = \frac{4.5}{m}$ 

Let 't' stand for "TIME"

So...
 $t = \frac{4}{s}$ 

Anything else?

> No.

I know that THERE ARE 2.2 POUNDS IN A KILOGRAM
I know that POTENTIAL ENERGY IS MASS TIMES 1 G TIMES HEIGHT
I know that POWER IS ENERGY OVER TIME

So...
 $2.2 = \frac{o}{k}$ 

So...
 $P = \frac{9.8 M h s s}{m}$ 

So...
 $p = \frac{e}{t}$ 

Hypothetically...

k = 1

Solving for o:

 $\begin{matrix} 2.2 & = & \frac{o}{k} \\ \frac{o}{k} & = & 2.2 \\ o \frac{1}{k} & = & 2.2 \\ o & = & 2.2 k \end{matrix}$ 
 o = 2.2 (or 11 / 5, or 2 & 1 / 5)

 $M = \frac{160}{o}$ 
 M = 72.7272727272727 (or 800 / 11, or 72 & 8 / 11)

Hypothetically...

m = 1

 $h = \frac{4.5}{m}$ 
 h = 4.5 (or 9 / 2, or 4 & 1 / 2)

Hypothetically...

s = 1

 $t = \frac{4}{s}$ 
 t = 4

 $P = \frac{9.8 M h s s}{m}$ 
 P = 3,207.27272727273

 $e = P$ 
 e = 3,207.27272727273

 $p = \frac{e}{t}$ 
 p = 801.818181818182

Solving for n:

 $\begin{matrix} \frac{1000 n s s s}{k m m} & = & p \\ n \frac{1000 s s s}{k m m} & = & p \\ 1000 n s s s & = & k m m p \\ n (1000 s s s) & = & k m m p \\ n & = & \frac{k m m p}{1000 s s s} \end{matrix}$ 
 n = 0.801818181818182 (or 441 / 550)

0.801818181818182 (or 441 / 550) is THE NUMBER.

Momentum: (momentum, mass, speed (or velocity, instantaneous speed, variable speed, or changing speed))

You enter...

If the momentum was 2,500[lb] x 65[mph], what would the speed in [mph] be if the mass were only 200[lb]?

AutoMathic understands...

Let 'm' stand for "MOMENTUM"

Let 'p' stand for "POUND"

Let 'M' stand for "MILE"

Let 'h' stand for "HOUR"

So...
 $m = \frac{162500 h}{M p}$ 

Let 's' stand for "SPEED"

(Find Ms/h)

Let 'a' stand for "MASS"

So...
 $a = \frac{200}{p}$ 

Anything else?

> No.

I know that MOMENTUM IS MASS TIMES SPEED

So...
 $m = a s$ 

Hypothetically...

h = 1

(Setting the free variable 'm' to 1)

m = 1

(Setting the free variable 'p' to 1)

p = 1

Solving for M:

 $\begin{matrix} m & = & \frac{162500 h}{M p} \\ \frac{162500 h}{M p} & = & m \\ 162500 h & = & M m p \\ M m p & = & 162500 h \\ M (m p) & = & 162500 h \\ M & = & \frac{162500 h}{m p} \end{matrix}$ 
 M = 162,500

 $a = \frac{200}{p}$ 
 a = 200

Solving for s:

 $\begin{matrix} m & = & a s \\ a s & = & m \\ s a & = & m \\ s & = & \frac{m}{a} \end{matrix}$ 
 s = 0.005 (or 1 / 200)

812.5 is THE SPEED IN [MPH].

Torque: (torque, force, radius)

You enter...

Calculate the torque in [N*m] when the radius is 18[cm], the mass is 132[lb], and acceleration is 1 G.

AutoMathic understands...

Let 't' stand for "TORQUE"

Let 'k' stand for "KILOGRAM"

Let 'm' stand for "METERS"

Let 's' stand for "SECOND"

(Find kmmt/(ss))

Let 'r' stand for "RADIUS"

Let 'c' stand for "CENTIMETER"

So...
 $r = \frac{18}{c}$ 

Let 'M' stand for "MASS"

Let 'p' stand for "POUND"

So...
 $M = \frac{132}{p}$ 

Let 'a' stand for "ACCELERATION"

So...
 $a = \frac{9.8 s s}{m}$ 

Anything else?

> No.

I know that THERE ARE A HUNDRED CENTIMETERS IN A METER
I know that THERE ARE 2.2 POUNDS IN A KILOGRAM
I know that FORCE IS MASS TIMES ACCELERATION
I know that TORQUE IS FORCE TIMES RADIUS

So...
 $100 = \frac{c}{m}$ 

So...
 $2.2 = \frac{p}{k}$ 

Let 'f' stand for "FORCE"

So...
 $f = M a$ 

So...
 $t = f r$ 

Hypothetically...

m = 1

Solving for c:

 $\begin{matrix} 100 & = & \frac{c}{m} \\ \frac{c}{m} & = & 100 \\ c \frac{1}{m} & = & 100 \\ c & = & 100 m \end{matrix}$ 
 c = 100

 $r = \frac{18}{c}$ 
 r = 0.18 (or 9 / 50)

Hypothetically...

s = 1

 $a = \frac{9.8 s s}{m}$ 
 a = 9.8 (or 49 / 5, or 9 & 4 / 5)

Hypothetically...

k = 1

Solving for p:

 $\begin{matrix} 2.2 & = & \frac{p}{k} \\ \frac{p}{k} & = & 2.2 \\ p \frac{1}{k} & = & 2.2 \\ p & = & 2.2 k \end{matrix}$ 
 p = 2.2 (or 11 / 5, or 2 & 1 / 5)

 $M = \frac{132}{p}$ 
 M = 60

 $f = M a$ 
 f = 588

 $t = f r$ 
 t = 105.84

105.84 is THE TORQUE IN [N * M].

Springs: (force, spring constant, displacement)

You enter...

Find the spring constant in [N/m] given that the mass is 200[kg], and the displacement is 3[cm]. Acceleration is 1 G.

AutoMathic understands...

Let 's' stand for "SPRING CONSTANT"

Let 'k' stand for "KILOGRAM"

Let 'm' stand for "METERS"

Let 'S' stand for "SECOND"

(Find ks/(SS))

Let 'M' stand for "MASS"

So...
 $M = \frac{200}{k}$ 

Let 'd' stand for "DISPLACEMENT"

Let 'c' stand for "CENTIMETER"

So...
 $d = \frac{3}{c}$ 

Let 'a' stand for "ACCELERATION"

So...
 $a = \frac{9.8 S S}{m}$ 

Anything else?

> No.

I know that THERE ARE A HUNDRED CENTIMETERS IN A METER
I know that FORCE IS MASS TIMES ACCELERATION
I know that FORCE = SPRING CONSTANT X DISPLACEMENT

So...
 $100 = \frac{c}{m}$ 

Let 'f' stand for "FORCE"

So...
 $f = M a$ 

So...
 $f = d s$ 

Hypothetically...

m = 1

Solving for c:

 $\begin{matrix} 100 & = & \frac{c}{m} \\ \frac{c}{m} & = & 100 \\ c \frac{1}{m} & = & 100 \\ c & = & 100 m \end{matrix}$ 
 c = 100

 $d = \frac{3}{c}$ 
 d = 0.03 (or 3 / 100)

Hypothetically...

S = 1

 $a = \frac{9.8 S S}{m}$ 
 a = 9.8 (or 49 / 5, or 9 & 4 / 5)

(Setting the free variable 'M' to 1)

M = 1

Solving for k:

 $\begin{matrix} M & = & \frac{200}{k} \\ \frac{200}{k} & = & M \\ 200 & = & M k \\ M k & = & 200 \\ k M & = & 200 \\ k & = & \frac{200}{M} \end{matrix}$ 
 k = 200

 $f = M a$ 
 f = 9.8 (or 49 / 5, or 9 & 4 / 5)

Solving for s:

 $\begin{matrix} f & = & d s \\ d s & = & f \\ s d & = & f \\ s & = & \frac{f}{d} \end{matrix}$ 
 s = 326.666666666667 (or 980 / 3, or 326 & 2 / 3)

65,333.3333333333 is THE SPRING CONSTANT IN [N / M].

Wave Motion: (wave speed, wavelength, frequency)

You enter...

If the wave speed is the speed of sound, and the frequency is F#, how many unit inches long is the wavelength?

AutoMathic understands...

Let 'w' stand for "WAVE SPEED"

Let 'f' stand for "FOOT"

Let 's' stand for "SECOND"

So...
 $w = \frac{1088 s}{f}$ 

Let 'F' stand for "FREQUENCY"

Let 'h' stand for "HERTZ"

So...
 $F = \frac{370}{h}$ 

Let 'n' stand for "NUMBER"

(Find n)

Let 'i' stand for "INCHES"

Let 'W' stand for "WAVELENGTH"

So...
 $\frac{n}{i} = W$ 

Anything else?

> No.

I know that THERE ARE TWELVE INCHES IN A FOOT
I know that HERTZ MEANS 1 / SECOND
I know that WAVE SPEED IS WAVELENGTH TIMES FREQUENCY
I know that DOPPLER FREQUENCY = FREQUENCY X WAVE SPEED / ( WAVE SPEED + RELATIVE SPEED )
I know that DOPPLER SHIFT IS THE DIFFERENCE BETWEEN DOPPLER FREQUENCY AND FREQUENCY

So...
 $12 = \frac{i}{f}$ 

So...
 $h = \frac{1}{s}$ 

So...
 $w = F W$ 

Let 'd' stand for "DOPPLER FREQUENCY"

Let 'r' stand for "RELATIVE SPEED"

So...
 $d = \frac{F w}{r + w}$ 

Let 'D' stand for "DOPPLER SHIFT"

So...
 $D = d - F$ 

Hypothetically...

f = 1

Solving for i:

 $\begin{matrix} 12 & = & \frac{i}{f} \\ \frac{i}{f} & = & 12 \\ i \frac{1}{f} & = & 12 \\ i & = & 12 f \end{matrix}$ 
 i = 12

Hypothetically...

w = 1

Solving for s:

 $\begin{matrix} w & = & \frac{1088 s}{f} \\ \frac{1088 s}{f} & = & w \\ s \frac{1088}{f} & = & w \\ 1088 s & = & f w \\ s (1088) & = & f w \\ s & = & \frac{f w}{1088} \end{matrix}$ 
 s = 0.000919117647058824

 $h = \frac{1}{s}$ 
 h = 1,088

 $F = \frac{370}{h}$ 
 F = 0.340073529411765 (or 185 / 544)

Solving for W:

 $\begin{matrix} w & = & F W \\ F W & = & w \\ W F & = & w \\ W & = & \frac{w}{F} \end{matrix}$ 
 W = 2.94054054054054 (or 544 / 185, or 2 & 174 / 185)

Solving for n:

 $\begin{matrix} \frac{n}{i} & = & W \\ n \frac{1}{i} & = & W \\ n & = & W i \end{matrix}$ 
 n = 35.2864864864865

35.2864864864865 is THE NUMBER.

Standing Waves: (length, wavelength, harmonic, overtone)

You enter...

If the length is 36[inches], and the overtone is two, how many unit cm long is the wavelength?

AutoMathic understands...

Let 'l' stand for "LENGTH"

Let 'i' stand for "INCHES"

So...
 $l = \frac{36}{i}$ 

Let 'o' stand for "OVERTONE"

 $o = 2$ 
 o = 2

Let 'n' stand for "NUMBER"

(Find n)

Let 'c' stand for "CENTIMETER"

Let 'w' stand for "WAVELENGTH"

So...
 $\frac{n}{c} = w$ 

Anything else?

> No.

I know that THERE ARE 2.54 CENTIMETERS PER INCH
I know that LENGTH IS THE HARMONIC TIMES WAVELENGTH OVER TWO
I know that THE OVERTONE IS ONE LESS THAN THE HARMONIC

So...
 $2.54 = \frac{c}{i}$ 

Let 'h' stand for "HARMONIC"

So...
 $l = \frac{h w}{2}$ 

So...
 $o = h - 1$ 

Solving for h:

 $\begin{matrix} o & = & - 1 + h \\ - 1 + h & = & o \\ h & = & 1 + o \end{matrix}$ 
 h = 3

Hypothetically...

i = 1

 $l = \frac{36}{i}$ 
 l = 36

Solving for c:

 $\begin{matrix} 2.54 & = & \frac{c}{i} \\ \frac{c}{i} & = & 2.54 \\ c \frac{1}{i} & = & 2.54 \\ c & = & 2.54 i \end{matrix}$ 
 c = 2.54 (or 127 / 50, or 2 & 27 / 50)

Solving for w:

 $\begin{matrix} l & = & \frac{h w}{2} \\ \frac{h w}{2} & = & l \\ w \frac{h}{2} & = & l \\ h w & = & 2 l \\ w h & = & 2 l \\ w & = & \frac{2 l}{h} \end{matrix}$ 
 w = 24

Solving for n:

 $\begin{matrix} \frac{n}{c} & = & w \\ n \frac{1}{c} & = & w \\ n & = & c w \end{matrix}$ 
 n = 60.96

60.96 is THE NUMBER.

Doppler Effect: (doppler frequency, frequency, wave speed, relative speed, doppler shift)

You enter...

Find the doppler shift in unit Hz. The wave speed is mach 1, the frequency is G natural, and the relative speed is 45[mph].

AutoMathic understands...

Let 'd' stand for "DOPPLER SHIFT"

Let 'h' stand for "HERTZ"

(Find dh)

Let 'w' stand for "WAVE SPEED"

Let 'f' stand for "FOOT"

Let 's' stand for "SECOND"

So...
 $w = \frac{1088 s}{f}$ 

Let 'F' stand for "FREQUENCY"

So...
 $F = \frac{392}{h}$ 

Let 'r' stand for "RELATIVE SPEED"

Let 'm' stand for "MILE"

Let 'H' stand for "HOUR"

So...
 $r = \frac{45 H}{m}$ 

Anything else?

> No.

I know that THERE ARE 5280 FEET IN A MILE
I know that THERE ARE SIXTY SECONDS IN A MINUTE
I know that THERE ARE SIXTY MINUTES IN AN HOUR
I know that HERTZ MEANS 1 / SECOND
I know that WAVE SPEED IS WAVELENGTH TIMES FREQUENCY
I know that DOPPLER FREQUENCY = FREQUENCY X WAVE SPEED / ( WAVE SPEED + RELATIVE SPEED )
I know that DOPPLER SHIFT IS THE DIFFERENCE BETWEEN DOPPLER FREQUENCY AND FREQUENCY

So...
 $5280 = \frac{f}{m}$ 

Let 'M' stand for "MINUTE"

So...
 $60 = \frac{s}{M}$ 

So...
 $60 = \frac{M}{H}$ 

So...
 $h = \frac{1}{s}$ 

Let 'W' stand for "WAVELENGTH"

So...
 $w = F W$ 

Let 'D' stand for "DOPPLER FREQUENCY"

So...
 $D = \frac{F w}{r + w}$ 

So...
 $d = D - F$ 

Hypothetically...

f = 1

Solving for m:

 $\begin{matrix} 5280 & = & \frac{f}{m} \\ \frac{f}{m} & = & 5280 \\ f & = & 5280 m \\ 5280 m & = & f \\ m (5280) & = & f \\ m & = & \frac{f}{5280} \end{matrix}$ 
 m = 0.000189393939393939

Hypothetically...

M = 1

Solving for s:

 $\begin{matrix} 60 & = & \frac{s}{M} \\ \frac{s}{M} & = & 60 \\ s \frac{1}{M} & = & 60 \\ s & = & 60 M \end{matrix}$ 
 s = 60

Solving for H:

 $\begin{matrix} 60 & = & \frac{M}{H} \\ \frac{M}{H} & = & 60 \\ M & = & 60 H \\ 60 H & = & M \\ H (60) & = & M \\ H & = & \frac{M}{60} \end{matrix}$ 
 H = 0.0166666666666667 (or 1 / 60)

 $h = \frac{1}{s}$ 
 h = 0.0166666666666667 (or 1 / 60)

 $w = \frac{1088 s}{f}$ 
 w = 65,280

 $F = \frac{392}{h}$ 
 F = 23,520

 $r = \frac{45 H}{m}$ 
 r = 3,960

Solving for W:

 $\begin{matrix} w & = & F W \\ F W & = & w \\ W F & = & w \\ W & = & \frac{w}{F} \end{matrix}$ 
 W = 2.77551020408163 (or 136 / 49, or 2 & 38 / 49)

 $D = \frac{F w}{r + w}$ 
 D = 22,174.835355286

 $d = D - F$ 
 d = -1,345.16464471404

-22.419410745234 is THE DOPPLER SHIFT IN UNIT HZ.

Capacitance: (capacitance, charge, voltage)

You enter...

How many trillionths of a unit Coulomb is the charge when the capacitance is 53[pF], and the voltage is 12[V]?

AutoMathic understands...

Let 'n' stand for "NUMBER"

(Find n)

Let 'c' stand for "COULOMB"

Let 'C' stand for "CHARGE"

So...
 $\frac{n}{1000000000000 c} = C$ 

Let 'a' stand for "CAPACITANCE"

Let 'p' stand for "PICOFARAD"

So...
 $a = \frac{53}{p}$ 

Let 'v' stand for "VOLTAGE"

Let 'V' stand for "VOLT"

So...
 $v = \frac{12}{V}$ 

Anything else?

> No.

I know that VOLTS = JOULES / COULOMB
I know that FARADS = COULOMBS PER VOLT
I know that THERE ARE A TRILLION PICOFARADS IN A FARAD
I know that CAPACITANCE IS CHARGE OVER VOLTAGE
I know that ELECTRICAL ENERGY IS CHARGE TIMES VOLTAGE

Let 'k' stand for "KILOGRAM"

Let 'm' stand for "METERS"

Let 's' stand for "SECOND"

So...
 $V = \frac{k m m}{c s s}$ 

Let 'f' stand for "FARADS"

So...
 $f = \frac{c}{V}$ 

So...
 $1000000000000 = \frac{p}{f}$ 

So...
 $a = \frac{C}{v}$ 

Let 'e' stand for "ELECTRICAL ENERGY"

So...
 $e = C v$ 

Hypothetically...

C = 1

Hypothetically...

V = 1

 $v = \frac{12}{V}$ 
 v = 12

 $a = \frac{C}{v}$ 
 a = 0.0833333333333333 (or 1 / 12)

 $e = C v$ 
 e = 12

Solving for p:

 $\begin{matrix} a & = & \frac{53}{p} \\ \frac{53}{p} & = & a \\ 53 & = & a p \\ a p & = & 53 \\ p a & = & 53 \\ p & = & \frac{53}{a} \end{matrix}$ 
 p = 636

Solving for f:

 $\begin{matrix} 1000000000000 & = & \frac{p}{f} \\ \frac{p}{f} & = & 1000000000000 \\ p & = & 1000000000000 f \\ 1000000000000 f & = & p \\ f (1000000000000) & = & p \\ f & = & \frac{p}{1000000000000} \end{matrix}$ 
 f = 0.000000000636

Solving for c:

 $\begin{matrix} f & = & \frac{c}{V} \\ \frac{c}{V} & = & f \\ c \frac{1}{V} & = & f \\ c & = & V f \end{matrix}$ 
 c = 0.000000000636

Solving for n:

 $\begin{matrix} \frac{n}{1000000000000 c} & = & C \\ n \frac{1}{1000000000000 c} & = & C \\ n & = & 1000000000000 C c \end{matrix}$ 
 n = 636

636 is THE NUMBER.

Electric Current: (current, charge, time)

You enter...

Calculate the charge measured in Coulombs when the current is 2.5[amps], and the time is 4[min].

AutoMathic understands...

Let 'c' stand for "CHARGE"

Let 'C' stand for "COULOMBS"

(Find Cc)

Let 'u' stand for "CURRENT"

Let 'a' stand for "AMPERE"

So...
 $u = \frac{2.5}{a}$ 

Let 't' stand for "TIME"

Let 'm' stand for "MINUTE"

So...
 $t = \frac{4}{m}$ 

Anything else?

> No.

I know that THERE ARE SIXTY SECONDS IN A MINUTE
I know that AMPERES = COULOMBS PER SECOND
I know that CURRENT IS CHARGE OVER TIME

Let 's' stand for "SECONDS"

So...
 $60 = \frac{s}{m}$ 

So...
 $a = \frac{C}{s}$ 

So...
 $u = \frac{c}{t}$ 

Hypothetically...

m = 1

 $t = \frac{4}{m}$ 
 t = 4

Solving for s:

 $\begin{matrix} 60 & = & \frac{s}{m} \\ \frac{s}{m} & = & 60 \\ s \frac{1}{m} & = & 60 \\ s & = & 60 m \end{matrix}$ 
 s = 60

(Setting the free variable 'u' to 1)

u = 1

Solving for a:

 $\begin{matrix} u & = & \frac{2.5}{a} \\ \frac{2.5}{a} & = & u \\ 2.5 & = & a u \\ a u & = & 2.5 \\ a u & = & 2.5 \\ a & = & \frac{2.5}{u} \end{matrix}$ 
 a = 2.5 (or 5 / 2, or 2 & 1 / 2)

Solving for C:

 $\begin{matrix} a & = & \frac{C}{s} \\ \frac{C}{s} & = & a \\ C \frac{1}{s} & = & a \\ C & = & a s \end{matrix}$ 
 C = 150

Solving for c:

 $\begin{matrix} u & = & \frac{c}{t} \\ \frac{c}{t} & = & u \\ c \frac{1}{t} & = & u \\ c & = & t u \end{matrix}$ 
 c = 4

600 is THE CHARGE MEASURED IN COULOMBS.

Resistance: (voltage, current, resistance)

You enter...

Given that voltage is 6[V], and the current is 300[mA], find the resistance measured in ohms.

AutoMathic understands...

Let 'v' stand for "VOLTAGE"

Let 'V' stand for "VOLT"

So...
 $v = \frac{6}{V}$ 

Let 'c' stand for "CURRENT"

Let 'm' stand for "MILLIAMPERE"

So...
 $c = \frac{300}{m}$ 

Let 'r' stand for "RESISTANCE"

Let 'o' stand for "OHMS"

(Find or)

Anything else?

> No.

I know that THERE ARE A THOUSAND MILLIAMPERES IN AN AMPERE
I know that OHMS = VOLTS / AMPERES
I know that VOLTAGE IS CURRENT TIMES RESISTANCE
I know that POWER IS CURRENT TIMES VOLTAGE. ASSUME KILOGRAMS=1; METERS=1

Let 'a' stand for "AMPERE"

So...
 $1000 = \frac{m}{a}$ 

So...
 $o = \frac{V}{a}$ 

So...
 $v = c r$ 

Let 'p' stand for "POWER"

So...
 $p = c v$ 

Let 'k' stand for "KILOGRAMS"

 $k = 1$ 
 k = 1

Let 'M' stand for "METERS"

 $M = 1$ 
 M = 1

Hypothetically...

a = 1

Solving for m:

 $\begin{matrix} 1000 & = & \frac{m}{a} \\ \frac{m}{a} & = & 1000 \\ m \frac{1}{a} & = & 1000 \\ m & = & 1000 a \end{matrix}$ 
 m = 1,000

 $c = \frac{300}{m}$ 
 c = 0.3 (or 3 / 10)

(Setting the free variable 'v' to 1)

v = 1

Solving for V:

 $\begin{matrix} v & = & \frac{6}{V} \\ \frac{6}{V} & = & v \\ 6 & = & V v \\ V v & = & 6 \\ V v & = & 6 \\ V & = & \frac{6}{v} \end{matrix}$ 
 V = 6

 $o = \frac{V}{a}$ 
 o = 6

Solving for r:

 $\begin{matrix} v & = & c r \\ c r & = & v \\ r c & = & v \\ r & = & \frac{v}{c} \end{matrix}$ 
 r = 3.33333333333333 (or 10 / 3, or 3 & 1 / 3)

 $p = c v$ 
 p = 0.3 (or 3 / 10)

20 is THE RESISTANCE MEASURED IN OHMS.

Electric Power: (power, current, voltage)

You enter...

If the power is 40[W], and the voltage is 12[V], find the resistance measured in ohms, and the current measured in amps.

AutoMathic understands...

Let 'p' stand for "POWER"

Let 'k' stand for "KILOGRAM"

Let 'm' stand for "METERS"

Let 's' stand for "SECOND"

So...
 $p = \frac{40 s s s}{k m m}$ 

Let 'v' stand for "VOLTAGE"

Let 'V' stand for "VOLT"

So...
 $v = \frac{12}{V}$ 

Let 'r' stand for "RESISTANCE"

Let 'o' stand for "OHMS"

(Find or)

Let 'c' stand for "CURRENT"

Let 'a' stand for "AMPERE"

(Find ac)

Anything else?

> No.

I know that AMPERES = COULOMBS PER SECOND
I know that VOLTS = JOULES / COULOMB
I know that OHMS = VOLTS / AMPERES
I know that FARADS = COULOMBS PER VOLT
I know that VOLTAGE IS CURRENT TIMES RESISTANCE
I know that POWER IS CURRENT TIMES VOLTAGE. ASSUME KILOGRAMS=1; METERS=1

Let 'C' stand for "COULOMBS"

So...
 $a = \frac{C}{s}$ 

So...
 $V = \frac{k m m}{C s s}$ 

So...
 $o = \frac{V}{a}$ 

Let 'f' stand for "FARADS"

So...
 $f = \frac{C}{V}$ 

So...
 $v = c r$ 

So...
 $p = c v$ 

 $k = 1$ 
 k = 1

 $m = 1$ 
 m = 1

Hypothetically...

s = 1

 $p = \frac{40 s s s}{k m m}$ 
 p = 40

Hypothetically...

a = 1

Solving for C:

 $\begin{matrix} a & = & \frac{C}{s} \\ \frac{C}{s} & = & a \\ C \frac{1}{s} & = & a \\ C & = & a s \end{matrix}$ 
 C = 1

 $V = \frac{k m m}{C s s}$ 
 V = 1

 $o = \frac{V}{a}$ 
 o = 1

 $f = \frac{C}{V}$ 
 f = 1

 $v = \frac{12}{V}$ 
 v = 12

Solving for c:

 $\begin{matrix} p & = & c v \\ c v & = & p \\ c v & = & p \\ c & = & \frac{p}{v} \end{matrix}$ 
 c = 3.33333333333333 (or 10 / 3, or 3 & 1 / 3)

Solving for r:

 $\begin{matrix} v & = & c r \\ c r & = & v \\ r c & = & v \\ r & = & \frac{v}{c} \end{matrix}$ 
 r = 3.6 (or 18 / 5, or 3 & 3 / 5)

3.6 (or 18 / 5, or 3 & 3 / 5) is THE RESISTANCE MEASURED IN OHMS.

3.33333333333333 (or 10 / 3, or 3 & 1 / 3) is THE CURRENT MEASURED IN AMPS.

Electrical Energy: (energy, charge, voltage)

You enter...

If the current is 15[Amps] when the voltage is 120[V], find the electrical energy in [kWh] when the time is 90[hr's].

AutoMathic understands...

Let 'c' stand for "CURRENT"

Let 'a' stand for "AMPERE"

So...
 $c = \frac{15}{a}$ 

Let 'v' stand for "VOLTAGE"

Let 'V' stand for "VOLT"

So...
 $v = \frac{120}{V}$ 

Let 'e' stand for "ELECTRICAL ENERGY"

Let 'k' stand for "KILOGRAM"

Let 'm' stand for "METERS"

Let 's' stand for "SECOND"

Let 'h' stand for "HOUR"

(Find ehkmm/(1000sss))

Let 't' stand for "TIME"

So...
 $t = \frac{90}{h}$ 

Anything else?

> No.

I know that THERE ARE SIXTY SECONDS IN A MINUTE
I know that THERE ARE SIXTY MINUTES IN AN HOUR
I know that POWER IS ENERGY OVER TIME
I know that AMPERES = COULOMBS PER SECOND
I know that VOLTS = JOULES / COULOMB
I know that OHMS = VOLTS / AMPERES
I know that FARADS = COULOMBS PER VOLT
I know that CURRENT IS CHARGE OVER TIME
I know that VOLTAGE IS CURRENT TIMES RESISTANCE
I know that CAPACITANCE IS CHARGE OVER VOLTAGE
I know that ELECTRICAL ENERGY IS CHARGE TIMES VOLTAGE
I know that POWER IS CURRENT TIMES VOLTAGE. ASSUME KILOGRAMS=1; METERS=1

Let 'M' stand for "MINUTE"

So...
 $60 = \frac{s}{M}$ 

So...
 $60 = \frac{M}{h}$ 

Let 'p' stand for "POWER"

Let 'E' stand for "ENERGY"

So...
 $p = \frac{E}{t}$ 

Let 'C' stand for "COULOMBS"

So...
 $a = \frac{C}{s}$ 

So...
 $V = \frac{k m m}{C s s}$ 

Let 'o' stand for "OHMS"

So...
 $o = \frac{V}{a}$ 

Let 'f' stand for "FARADS"

So...
 $f = \frac{C}{V}$ 

Let 'H' stand for "CHARGE"

So...
 $c = \frac{H}{t}$ 

Let 'r' stand for "RESISTANCE"

So...
 $v = c r$ 

Let 'A' stand for "CAPACITANCE"

So...
 $A = \frac{H}{v}$ 

So...
 $e = H v$ 

So...
 $p = c v$ 

 $k = 1$ 
 k = 1

 $m = 1$ 
 m = 1

Hypothetically...

M = 1

Solving for s:

 $\begin{matrix} 60 & = & \frac{s}{M} \\ \frac{s}{M} & = & 60 \\ s \frac{1}{M} & = & 60 \\ s & = & 60 M \end{matrix}$ 
 s = 60

Solving for h:

 $\begin{matrix} 60 & = & \frac{M}{h} \\ \frac{M}{h} & = & 60 \\ M & = & 60 h \\ 60 h & = & M \\ h (60) & = & M \\ h & = & \frac{M}{60} \end{matrix}$ 
 h = 0.0166666666666667 (or 1 / 60)

 $t = \frac{90}{h}$ 
 t = 5,400

Hypothetically...

a = 1

 $c = \frac{15}{a}$ 
 c = 15

Solving for C:

 $\begin{matrix} a & = & \frac{C}{s} \\ \frac{C}{s} & = & a \\ C \frac{1}{s} & = & a \\ C & = & a s \end{matrix}$ 
 C = 60

 $V = \frac{k m m}{C s s}$ 
 V = 0.00000462962962962963

 $o = \frac{V}{a}$ 
 o = 0.00000462962962962963

 $f = \frac{C}{V}$ 
 f = 12,960,000

Solving for H:

 $\begin{matrix} c & = & \frac{H}{t} \\ \frac{H}{t} & = & c \\ H \frac{1}{t} & = & c \\ H & = & c t \end{matrix}$ 
 H = 81,000

 $v = \frac{120}{V}$ 
 v = 25,920,000

Solving for r:

 $\begin{matrix} v & = & c r \\ c r & = & v \\ r c & = & v \\ r & = & \frac{v}{c} \end{matrix}$ 
 r = 1,728,000

 $A = \frac{H}{v}$ 
 A = 0.003125 (or 1 / 320)

 $e = H v$ 
 e = 2,099,520,000,000

 $p = c v$ 
 p = 388,800,000

Solving for E:

 $\begin{matrix} p & = & \frac{E}{t} \\ \frac{E}{t} & = & p \\ E \frac{1}{t} & = & p \\ E & = & p t \end{matrix}$ 
 E = 2,099,520,000,000

162 is THE ELECTRICAL ENERGY IN [KWH].

Chemistry Measurement: (Avogadro's number, particles, moles)

You enter...

Find the mass per particle measured in amu, when the mass for 6 moles is 84[gm].

AutoMathic understands...

Let 'm' stand for "MASS"

Let 'p' stand for "PARTICLE"

Let 'a' stand for "AMU"

(Find am/p)

Let 'M' stand for "MOLES"

Let 'g' stand for "GRAM"

So...
 $\frac{6 m}{M} = \frac{84}{g}$ 

Anything else?

> No.

I know that AVOGADRO'S NUMBER IS THE NUMBER OF PARTICLES PER MOLE
I know that MOLES IS GRAMS / FORMULA WEIGHT
I know that AVOGADRO'S NUMBER IS THE NUMBER OF AMU PER GRAM

So...
 $602200000000000000000000 = \frac{p}{M}$ 

Let 'f' stand for "FORMULA WEIGHT"

So...
 $M = \frac{g}{f}$ 

So...
 $602200000000000000000000 = \frac{a}{g}$ 

Hypothetically...

p = 1

Solving for M:

 $\begin{matrix} 602200000000000000000000 & = & \frac{p}{M} \\ \frac{p}{M} & = & 602200000000000000000000 \\ p & = & 602200000000000000000000 M \\ 602200000000000000000000 M & = & p \\ M (602200000000000000000000) & = & p \\ M & = & \frac{p}{602200000000000000000000} \end{matrix}$ 
 M = 0.00000000000000000000000166057788110262

Hypothetically...

f = 1

Solving for g:

 $\begin{matrix} M & = & \frac{g}{f} \\ \frac{g}{f} & = & M \\ g \frac{1}{f} & = & M \\ g & = & M f \end{matrix}$ 
 g = 0.00000000000000000000000166057788110262

Solving for a:

 $\begin{matrix} 602200000000000000000000 & = & \frac{a}{g} \\ \frac{a}{g} & = & 602200000000000000000000 \\ a \frac{1}{g} & = & 602200000000000000000000 \\ a & = & 602200000000000000000000 g \end{matrix}$ 
 a = 1

Solving for m:

 $\begin{matrix} \frac{6 m}{M} & = & \frac{84}{g} \\ m \frac{6}{M} & = & \frac{84}{g} \\ 6 m & = & \frac{84 M}{g} \\ m (6) & = & \frac{84 M}{g} \\ m & = & \frac{14 M}{g} \end{matrix}$ 
 m = 14

14 is THE MASS PER PARTICLE MEASURED IN AMU.

Molarity: (moles, molarity or molar concentration, molecular/formula weight)

You enter...

If the formula weight is 106, find the number of grams such that the molar concentration is 4 when the number of ml is 1,500.

AutoMathic understands...

Let 'f' stand for "FORMULA WEIGHT"

 $f = 106$ 
 f = 106

Let 'g' stand for "GRAMS"

(Find g)

Let 'm' stand for "MOLARITY"

 $m = 4$ 
 m = 4

Let 'M' stand for "MILLILITER"

 $M = 1500$ 
 M = 1,500

Anything else?

> No.

I know that THERE ARE A THOUSAND MILLILITERS IN A LITER
I know that MOLARITY IS MOLES PER LITER
I know that MOLES IS GRAMS / FORMULA WEIGHT
I know that SPECIFIC GRAVITY = DENSITY / (1 [GRAM/ML])
I know that PRESSURE IN [ATM] X VOLUME IN [L] = MOLES X 0.0821 X TEMPERATURE IN [KELVIN]
I know that HEAT ENERGY IN [JOULES] IS 3/2 X MOLES X 8.314 X TEMPERATURE IN [KELVIN]. ASSUME SECONDS=1; METERS=1

Let 'l' stand for "LITER"

So...
 $1000 = \frac{M}{l}$ 

Solving for l:

 $\begin{matrix} 1000 & = & \frac{M}{l} \\ \frac{M}{l} & = & 1000 \\ M & = & 1000 l \\ 1000 l & = & M \\ l (1000) & = & M \\ l & = & \frac{M}{1000} \end{matrix}$ 
 l = 1.5 (or 3 / 2, or 1 & 1 / 2)

Let 'o' stand for "MOLES"

So...
 $m = \frac{o}{l}$ 

Solving for o:

 $\begin{matrix} m & = & \frac{o}{l} \\ \frac{o}{l} & = & m \\ o \frac{1}{l} & = & m \\ o & = & l m \end{matrix}$ 
 o = 6

So...
 $o = \frac{g}{f}$ 

Solving for g:

 $\begin{matrix} o & = & \frac{g}{f} \\ \frac{g}{f} & = & o \\ g \frac{1}{f} & = & o \\ g & = & f o \end{matrix}$ 
 g = 636

Let 's' stand for "SPECIFIC GRAVITY"

Let 'd' stand for "DENSITY"

So...
 $s = \frac{d g}{M}$ 

Let 'p' stand for "PRESSURE"

Let 'a' stand for "ATMOSPHERE"

Let 'v' stand for "VOLUME"

Let 't' stand for "TEMPERATURE"

Let 'k' stand for "KELVIN"

So...
 $a l p v = 0.0821 k o t$ 

Let 'h' stand for "HEAT ENERGY"

Let 'K' stand for "KILOGRAM"

Let 'e' stand for "METERS"

Let 'S' stand for "SECOND"

So...
 $\frac{K e e h}{S S} = \frac{3 (8.314) k o t}{2}$ 

 $S = 1$ 
 S = 1

 $e = 1$ 
 e = 1

636 is THE NUMBER OF GRAMS.

Density: (density, mass, volume)

You enter...

If the density is half the density of steel, and 75% of the volume is 2[gal], find the mass measured in pounds.

AutoMathic understands...

Let 'd' stand for "DENSITY"

Let 'g' stand for "GRAM"

Let 'm' stand for "MILLILITER"

So...
 $d = \frac{7.8 m}{2 g}$ 

Let 'v' stand for "VOLUME"

Let 'G' stand for "GALLON"

So...
 $\frac{3 v}{4} = \frac{2}{G}$ 

Let 'M' stand for "MASS"

Let 'p' stand for "POUNDS"

(Find Mp)

Anything else?

> No.

I know that THERE ARE 2.2 POUNDS IN A KILOGRAM
I know that THERE ARE A THOUSAND GRAMS IN A KILOGRAM
I know that THERE ARE 3.785 LITERS IN A GALLON
I know that THERE ARE A THOUSAND MILLILITERS IN A LITER
I know that DENSITY IS THE RATIO OF MASS TO VOLUME
I know that SPECIFIC GRAVITY = DENSITY / (1 [GRAM/ML])

Let 'k' stand for "KILOGRAM"

So...
 $2.2 = \frac{p}{k}$ 

So...
 $1000 = \frac{g}{k}$ 

Let 'l' stand for "LITERS"

So...
 $3.785 = \frac{l}{G}$ 

So...
 $1000 = \frac{m}{l}$ 

So...
 $d = \frac{M}{v}$ 

Let 's' stand for "SPECIFIC GRAVITY"

So...
 $s = \frac{d g}{m}$ 

Hypothetically...

g = 1

Solving for k:

 $\begin{matrix} 1000 & = & \frac{g}{k} \\ \frac{g}{k} & = & 1000 \\ g & = & 1000 k \\ 1000 k & = & g \\ k (1000) & = & g \\ k & = & \frac{g}{1000} \end{matrix}$ 
 k = 0.001

Solving for p:

 $\begin{matrix} 2.2 & = & \frac{p}{k} \\ \frac{p}{k} & = & 2.2 \\ p \frac{1}{k} & = & 2.2 \\ p & = & 2.2 k \end{matrix}$ 
 p = 0.0022

Hypothetically...

G = 1

Solving for v:

 $\begin{matrix} \frac{3 v}{4} & = & \frac{2}{G} \\ v \frac{3}{4} & = & \frac{2}{G} \\ 3 v & = & \frac{8}{G} \\ v (3) & = & \frac{8}{G} \\ v & = & \frac{8}{3 G} \end{matrix}$ 
 v = 2.66666666666667 (or 8 / 3, or 2 & 2 / 3)

Solving for l:

 $\begin{matrix} 3.785 & = & \frac{l}{G} \\ \frac{l}{G} & = & 3.785 \\ l \frac{1}{G} & = & 3.785 \\ l & = & 3.785 G \end{matrix}$ 
 l = 3.785 (or 757 / 200, or 3 & 157 / 200)

Solving for m:

 $\begin{matrix} 1000 & = & \frac{m}{l} \\ \frac{m}{l} & = & 1000 \\ m \frac{1}{l} & = & 1000 \\ m & = & 1000 l \end{matrix}$ 
 m = 3,785

 $d = \frac{7.8 m}{2 g}$ 
 d = 14,761.5

Solving for M:

 $\begin{matrix} d & = & \frac{M}{v} \\ \frac{M}{v} & = & d \\ M \frac{1}{v} & = & d \\ M & = & d v \end{matrix}$ 
 M = 39,364

 $s = \frac{d g}{m}$ 
 s = 3.9 (or 39 / 10, or 3 & 9 / 10)

86.6008 is THE MASS MEASURED IN POUNDS.

Specific Gravity: (specific gravity, density)

You enter...

If the specific gravity is 0.668, find the density measured in lb/gal.

AutoMathic understands...

Let 's' stand for "SPECIFIC GRAVITY"

 $s = 0.668$ 
 s = 0.668 (or 167 / 250)

Let 'd' stand for "DENSITY"

Let 'p' stand for "POUND"

Let 'g' stand for "GALLON"

(Find dp/g)

Anything else?

> No.

I know that THERE ARE 2.2 POUNDS IN A KILOGRAM
I know that THERE ARE A THOUSAND GRAMS IN A KILOGRAM
I know that THERE ARE 3.785 LITERS IN A GALLON
I know that THERE ARE A THOUSAND MILLILITERS IN A LITER
I know that SPECIFIC GRAVITY = DENSITY / (1 [GRAM/ML])

Let 'k' stand for "KILOGRAM"

So...
 $2.2 = \frac{p}{k}$ 

Let 'G' stand for "GRAMS"

So...
 $1000 = \frac{G}{k}$ 

Let 'l' stand for "LITERS"

So...
 $3.785 = \frac{l}{g}$ 

Let 'm' stand for "MILLILITERS"

So...
 $1000 = \frac{m}{l}$ 

So...
 $s = \frac{G d}{m}$ 

Hypothetically...

g = 1

Solving for l:

 $\begin{matrix} 3.785 & = & \frac{l}{g} \\ \frac{l}{g} & = & 3.785 \\ l \frac{1}{g} & = & 3.785 \\ l & = & 3.785 g \end{matrix}$ 
 l = 3.785 (or 757 / 200, or 3 & 157 / 200)

Solving for m:

 $\begin{matrix} 1000 & = & \frac{m}{l} \\ \frac{m}{l} & = & 1000 \\ m \frac{1}{l} & = & 1000 \\ m & = & 1000 l \end{matrix}$ 
 m = 3,785

Hypothetically...

k = 1

Solving for p:

 $\begin{matrix} 2.2 & = & \frac{p}{k} \\ \frac{p}{k} & = & 2.2 \\ p \frac{1}{k} & = & 2.2 \\ p & = & 2.2 k \end{matrix}$ 
 p = 2.2 (or 11 / 5, or 2 & 1 / 5)

Solving for G:

 $\begin{matrix} 1000 & = & \frac{G}{k} \\ \frac{G}{k} & = & 1000 \\ G \frac{1}{k} & = & 1000 \\ G & = & 1000 k \end{matrix}$ 
 G = 1,000

Solving for d:

 $\begin{matrix} s & = & \frac{G d}{m} \\ \frac{G d}{m} & = & s \\ d \frac{G}{m} & = & s \\ G d & = & m s \\ d G & = & m s \\ d & = & \frac{m s}{G} \end{matrix}$ 
 d = 2.52838

5.562436 is THE DENSITY MEASURED IN LB / GAL.

Atomic / Molecular / Chemical Properties: (atoms, protons, neutrons, nucleons, electrons, atomic number, mass number, ionic number/charge, atomic weight/mass, molecular/formula weight)

You enter...

Find the number of nucleons, and the atomic weight. The atomic number is 6, the ratio of protons to neutrons is 1:1, and the ionic charge is +2.

AutoMathic understands...

Let 'n' stand for "NUCLEONS"

(Find n)

Let 'f' stand for "FORMULA WEIGHT"

(Find f)

Let 'a' stand for "ATOMIC NUMBER"

 $a = 6$ 
 a = 6

Let 'p' stand for "PROTONS"

Let 'N' stand for "NEUTRONS"

So...
 $\frac{p}{N} = 1$ 

Let 'i' stand for "IONIC NUMBER"

 $i = 2$ 
 i = 2

Anything else?

> No.

I know that ATOMIC NUMBER IS THE NUMBER OF PROTONS IN AN ATOM
I know that MASS NUMBER IS THE SUM OF THE ATOMIC NUMBER AND NEUTRONS IN THE ATOM
I know that MASS NUMBER IS THE NUMBER OF NUCLEONS
I know that IONIC NUMBER IS THE DIFFERENCE BETWEEN THE NUMBER OF PROTONS PER ATOM AND ELECTRONS PER ATOM
I know that ATOMIC WEIGHT X ATOMS = 1.007276 X PROTONS + 1.008665 X NEUTRONS + 0.0005486 X ELECTRONS

Let 'A' stand for "ATOM"

So...
 $a = \frac{p}{A}$ 

Let 'm' stand for "MASS NUMBER"

So...
 $m = \frac{N}{A} + a$ 

So...
 $m = n$ 

Let 'e' stand for "ELECTRONS"

So...
 $i = \frac{p - e}{A}$ 

So...
 $A f = 0.0005486 e + 1.007276 p + 1.008665 N$ 

Hypothetically...

N = 1

Solving for p:

 $\begin{matrix} \frac{p}{N} & = & 1 \\ p \frac{1}{N} & = & 1 \\ p & = & N \end{matrix}$ 
 p = 1

Solving for A:

 $\begin{matrix} a & = & \frac{p}{A} \\ \frac{p}{A} & = & a \\ p & = & A a \\ A a & = & p \\ A a & = & p \\ A & = & \frac{p}{a} \end{matrix}$ 
 A = 0.166666666666667 (or 1 / 6)

 $m = \frac{N}{A} + a$ 
 m = 12

Solving for n:

 $\begin{matrix} m & = & n \\ n & = & m \end{matrix}$ 
 n = 12

Solving for e:

 $\begin{matrix} i & = & \frac{p - e}{A} \\ \frac{p - e}{A} & = & i \\ \frac{p}{A} - \frac{e}{A} & = & i \\ - \frac{e}{A} & = & i - \frac{p}{A} \\ e (- \frac{1}{A}) & = & i - \frac{p}{A} \\ \frac{e}{A} & = & \frac{p}{A} - i \\ e \frac{1}{A} & = & \frac{p}{A} - i \\ e & = & p - A i \end{matrix}$ 
 e = 0.666666666666667 (or 2 / 3)

Solving for f:

 $\begin{matrix} A f & = & 0.0005486 e + 1.007276 p + 1.008665 N \\ f A & = & 0.0005486 e + 1.007276 p + 1.008665 N \\ f & = & \frac{0.0005486 e + 1.007276 p + 1.008665 N}{A} \end{matrix}$ 
 f = 12.0978404

12 is THE NUMBER OF NUCLEONS.

12.0978404 is THE ATOMIC WEIGHT.

Ideal Gas Law: (pressure, volume, moles, temperature)

You enter...

Compute the volume measured in liters, if the number of moles is 1, pressure is standard pressure, and temperature is standard temperature.

AutoMathic understands...

Let 'v' stand for "VOLUME"

Let 'l' stand for "LITERS"

(Find lv)

Let 'm' stand for "MOLES"

 $m = 1$ 
 m = 1

Let 'p' stand for "PRESSURE"

Let 'a' stand for "ATMOSPHERE"

So...
 $p = \frac{1}{a}$ 

Let 't' stand for "TEMPERATURE"

Let 'k' stand for "KELVIN"

So...
 $t = \frac{273.159}{k}$ 

Anything else?

> No.

I know that THERE ARE A THOUSAND MILLILITERS IN A LITER
I know that MOLARITY IS MOLES PER LITER
I know that MOLES IS GRAMS / FORMULA WEIGHT
I know that DENSITY IS THE RATIO OF MASS TO VOLUME
I know that SPECIFIC GRAVITY = DENSITY / (1 [GRAM/ML])
I know that PRESSURE IN [ATM] X VOLUME IN [L] = MOLES X 0.0821 X TEMPERATURE IN [KELVIN]
I know that HEAT ENERGY IN [JOULES] IS 3/2 X MOLES X 8.314 X TEMPERATURE IN [KELVIN]. ASSUME SECONDS=1; METERS=1

Let 'M' stand for "MILLILITERS"

So...
 $1000 = \frac{M}{l}$ 

Let 'o' stand for "MOLARITY"

So...
 $o = \frac{m}{l}$ 

Let 'g' stand for "GRAMS"

Let 'f' stand for "FORMULA WEIGHT"

So...
 $m = \frac{g}{f}$ 

Let 'd' stand for "DENSITY"

Let 'A' stand for "MASS"

So...
 $d = \frac{A}{v}$ 

Let 's' stand for "SPECIFIC GRAVITY"

So...
 $s = \frac{d g}{M}$ 

So...
 $a l p v = 0.0821 k m t$ 

Let 'h' stand for "HEAT ENERGY"

Let 'K' stand for "KILOGRAM"

Let 'e' stand for "METERS"

Let 'S' stand for "SECOND"

So...
 $\frac{K e e h}{S S} = \frac{3 (8.314) k m t}{2}$ 

 $S = 1$ 
 S = 1

 $e = 1$ 
 e = 1

Hypothetically...

l = 1

Solving for M:

 $\begin{matrix} 1000 & = & \frac{M}{l} \\ \frac{M}{l} & = & 1000 \\ M \frac{1}{l} & = & 1000 \\ M & = & 1000 l \end{matrix}$ 
 M = 1,000

 $o = \frac{m}{l}$ 
 o = 1

(Setting the free variable 'p' to 1)

p = 1

Solving for a:

 $\begin{matrix} p & = & \frac{1}{a} \\ \frac{1}{a} & = & p \\ 1 & = & a p \\ a p & = & 1 \\ a p & = & 1 \\ a & = & \frac{1}{p} \end{matrix}$ 
 a = 1

(Setting the free variable 't' to 1)

t = 1

Solving for k:

 $\begin{matrix} t & = & \frac{273.159}{k} \\ \frac{273.159}{k} & = & t \\ 273.159 & = & k t \\ k t & = & 273.159 \\ k t & = & 273.159 \\ k & = & \frac{273.159}{t} \end{matrix}$ 
 k = 273.159

Solving for v:

 $\begin{matrix} a l p v & = & 0.0821 k m t \\ v (a l p) & = & 0.0821 k m t \\ v & = & \frac{0.0821 k m t}{a l p} \end{matrix}$ 
 v = 22.4263539

22.4263539 is THE VOLUME MEASURED IN LITERS.

Heat Energy of an Ideal Gas: (heat energy, moles, temperature)

You enter...

Calculate the heat energy in [J] when the number of moles is 5, and the temperature is room temperature.

AutoMathic understands...

Let 'h' stand for "HEAT ENERGY"

Let 'k' stand for "KILOGRAM"

Let 'm' stand for "METERS"

Let 's' stand for "SECOND"

(Find hkmm/(ss))

Let 'M' stand for "MOLES"

 $M = 5$ 
 M = 5

Let 't' stand for "TEMPERATURE"

Let 'K' stand for "KELVIN"

So...
 $t = \frac{293}{K}$ 

Anything else?

> No.

I know that THERE ARE A THOUSAND GRAMS IN A KILOGRAM
I know that THERE ARE A THOUSAND MILLILITERS IN A LITER
I know that MOLARITY IS MOLES PER LITER
I know that MOLES IS GRAMS / FORMULA WEIGHT
I know that SPECIFIC GRAVITY = DENSITY / (1 [GRAM/ML])
I know that PRESSURE IN [ATM] X VOLUME IN [L] = MOLES X 0.0821 X TEMPERATURE IN [KELVIN]
I know that HEAT ENERGY IN [JOULES] IS 3/2 X MOLES X 8.314 X TEMPERATURE IN [KELVIN]. ASSUME SECONDS=1; METERS=1

Let 'g' stand for "GRAMS"

So...
 $1000 = \frac{g}{k}$ 

Let 'i' stand for "MILLILITERS"

Let 'l' stand for "LITER"

So...
 $1000 = \frac{i}{l}$ 

Let 'o' stand for "MOLARITY"

So...
 $o = \frac{M}{l}$ 

Let 'f' stand for "FORMULA WEIGHT"

So...
 $M = \frac{g}{f}$ 

Let 'S' stand for "SPECIFIC GRAVITY"

Let 'd' stand for "DENSITY"

So...
 $S = \frac{d g}{i}$ 

Let 'p' stand for "PRESSURE"

Let 'a' stand for "ATMOSPHERE"

Let 'v' stand for "VOLUME"

So...
 $a l p v = 0.0821 K M t$ 

So...
 $\frac{h k m m}{s s} = \frac{3 (8.314) K M t}{2}$ 

 $s = 1$ 
 s = 1

 $m = 1$ 
 m = 1

Hypothetically...

k = 1

Solving for g:

 $\begin{matrix} 1000 & = & \frac{g}{k} \\ \frac{g}{k} & = & 1000 \\ g \frac{1}{k} & = & 1000 \\ g & = & 1000 k \end{matrix}$ 
 g = 1,000

Solving for f:

 $\begin{matrix} M & = & \frac{g}{f} \\ \frac{g}{f} & = & M \\ g & = & M f \\ M f & = & g \\ f M & = & g \\ f & = & \frac{g}{M} \end{matrix}$ 
 f = 200

Hypothetically...

l = 1

Solving for i:

 $\begin{matrix} 1000 & = & \frac{i}{l} \\ \frac{i}{l} & = & 1000 \\ i \frac{1}{l} & = & 1000 \\ i & = & 1000 l \end{matrix}$ 
 i = 1,000

 $o = \frac{M}{l}$ 
 o = 5

(Setting the free variable 't' to 1)

t = 1

Solving for K:

 $\begin{matrix} t & = & \frac{293}{K} \\ \frac{293}{K} & = & t \\ 293 & = & K t \\ K t & = & 293 \\ K t & = & 293 \\ K & = & \frac{293}{t} \end{matrix}$ 
 K = 293

Solving for h:

 $\begin{matrix} \frac{h k m m}{s s} & = & \frac{3 (8.314) K M t}{2} \\ h \frac{k m m}{s s} & = & \frac{3 (8.314) K M t}{2} \\ h k m m & = & \frac{3 (8.314) K M s s t}{2} \\ h (k m m) & = & \frac{3 (8.314) K M s s t}{2} \\ h & = & \frac{3 (8.314) K M s s t}{2 k m m} \end{matrix}$ 
 h = 18,270.015

18,270.015 is THE HEAT ENERGY IN [J].

Specific Heat: (specific heat, heat energy, mass, deltaT)

You enter...

Find the heat energy measured in Joules given that the mass is 7.05[gm], deltaT is 75, and the specific heat is the specific heat of iron.

AutoMathic understands...

Let 'h' stand for "HEAT ENERGY"

Let 'k' stand for "KILOGRAM"

Let 'm' stand for "METERS"

Let 's' stand for "SECOND"

(Find hkmm/(ss))

Let 'M' stand for "MASS"

Let 'g' stand for "GRAM"

So...
 $M = \frac{7.05}{g}$ 

Let 'd' stand for "DELTAT"

 $d = 75$ 
 d = 75

Let 'S' stand for "SPECIFIC HEAT"

So...
 $S = \frac{450 s s}{m m}$ 

Anything else?

> No.

I know that THERE ARE A THOUSAND GRAMS IN A KILOGRAM
I know that THERE ARE A THOUSAND MILLILITERS IN A LITER
I know that MOLARITY IS MOLES PER LITER
I know that MOLES IS GRAMS / FORMULA WEIGHT
I know that SPECIFIC GRAVITY = DENSITY / (1 [GRAM/ML])
I know that PRESSURE IN [ATM] X VOLUME IN [L] = MOLES X 0.0821 X TEMPERATURE IN [KELVIN]
I know that HEAT ENERGY IN [JOULES] IS 3/2 X MOLES X 8.314 X TEMPERATURE IN [KELVIN]. ASSUME SECONDS=1; METERS=1
I know that HEAT ENERGY IS SPECIFIC HEAT TIMES MASS TIMES DELTAT. ASSUME SECONDS=1; METERS=1

So...
 $1000 = \frac{g}{k}$ 

Let 'i' stand for "MILLILITERS"

Let 'l' stand for "LITER"

So...
 $1000 = \frac{i}{l}$ 

Let 'o' stand for "MOLARITY"

Let 'O' stand for "MOLES"

So...
 $o = \frac{O}{l}$ 

Let 'f' stand for "FORMULA WEIGHT"

So...
 $O = \frac{g}{f}$ 

Let 'p' stand for "SPECIFIC GRAVITY"

Let 'D' stand for "DENSITY"

So...
 $p = \frac{D g}{i}$ 

Let 'P' stand for "PRESSURE"

Let 'a' stand for "ATMOSPHERE"

Let 'v' stand for "VOLUME"

Let 't' stand for "TEMPERATURE"

Let 'K' stand for "KELVIN"

So...
 $P a l v = 0.0821 K O t$ 

So...
 $\frac{h k m m}{s s} = \frac{3 (8.314) K O t}{2}$ 

 $s = 1$ 
 s = 1

 $m = 1$ 
 m = 1

 $S = \frac{450 s s}{m m}$ 
 S = 450

So...
 $h = M S d$ 

 $s = 1$ 
 s = 1

Undefining 'S' ...

Undefining 'm' ...

 $m = 1$ 
 m = 1

 $S = \frac{450 s s}{m m}$ 
 S = 450

Hypothetically...

k = 1

Solving for g:

 $\begin{matrix} 1000 & = & \frac{g}{k} \\ \frac{g}{k} & = & 1000 \\ g \frac{1}{k} & = & 1000 \\ g & = & 1000 k \end{matrix}$ 
 g = 1,000

 $M = \frac{7.05}{g}$ 
 M = 0.00705

 $h = M S d$ 
 h = 237.9375

237.9375 is THE HEAT ENERGY MEASURED IN JOULES.

Heat Capacity: (heat capacity, specific heat, mass)

You enter...

What's the heat capacity in [kJ] when the volume is 4[L], the density is the density of water, and the specific heat is the specific heat of water?

AutoMathic understands...

Let 'h' stand for "HEAT CAPACITY"

Let 'k' stand for "KILOGRAM"

Let 'm' stand for "METERS"

Let 's' stand for "SECOND"

(Find hkmm/(1000ss))

Let 'v' stand for "VOLUME"

Let 'l' stand for "LITER"

So...
 $v = \frac{4}{l}$ 

Let 'd' stand for "DENSITY"

Let 'g' stand for "GRAM"

Let 'M' stand for "MILLILITER"

So...
 $d = \frac{M}{g}$ 

Let 'S' stand for "SPECIFIC HEAT"

So...
 $S = \frac{4180 s s}{m m}$ 

Anything else?

> No.

I know that THERE ARE A THOUSAND GRAMS IN A KILOGRAM
I know that THERE ARE A THOUSAND MILLILITERS IN A LITER
I know that MOLARITY IS MOLES PER LITER
I know that MOLES IS GRAMS / FORMULA WEIGHT
I know that DENSITY IS THE RATIO OF MASS TO VOLUME
I know that SPECIFIC GRAVITY = DENSITY / (1 [GRAM/ML])
I know that PRESSURE IN [ATM] X VOLUME IN [L] = MOLES X 0.0821 X TEMPERATURE IN [KELVIN]
I know that HEAT ENERGY IN [JOULES] IS 3/2 X MOLES X 8.314 X TEMPERATURE IN [KELVIN]. ASSUME SECONDS=1; METERS=1
I know that HEAT ENERGY IS SPECIFIC HEAT TIMES MASS TIMES DELTAT. ASSUME SECONDS=1; METERS=1
I know that HEAT CAPACITY IS MASS TIMES SPECIFIC HEAT

So...
 $1000 = \frac{g}{k}$ 

So...
 $1000 = \frac{M}{l}$ 

Let 'o' stand for "MOLARITY"

Let 'O' stand for "MOLES"

So...
 $o = \frac{O}{l}$ 

Let 'f' stand for "FORMULA WEIGHT"

So...
 $O = \frac{g}{f}$ 

Let 'a' stand for "MASS"

So...
 $d = \frac{a}{v}$ 

Let 'p' stand for "SPECIFIC GRAVITY"

So...
 $p = \frac{d g}{M}$ 

Let 'P' stand for "PRESSURE"

Let 'A' stand for "ATMOSPHERE"

Let 't' stand for "TEMPERATURE"

Let 'K' stand for "KELVIN"

So...
 $A P l v = 0.0821 K O t$ 

Let 'H' stand for "HEAT ENERGY"

So...
 $\frac{H k m m}{s s} = \frac{3 (8.314) K O t}{2}$ 

 $s = 1$ 
 s = 1

 $m = 1$ 
 m = 1

 $S = \frac{4180 s s}{m m}$ 
 S = 4,180

Let 'D' stand for "DELTAT"

So...
 $H = D S a$ 

 $s = 1$ 
 s = 1

Undefining 'S' ...

Undefining 'm' ...

 $m = 1$ 
 m = 1

 $S = \frac{4180 s s}{m m}$ 
 S = 4,180

So...
 $h = S a$ 

Hypothetically...

g = 1

Solving for k:

 $\begin{matrix} 1000 & = & \frac{g}{k} \\ \frac{g}{k} & = & 1000 \\ g & = & 1000 k \\ 1000 k & = & g \\ k (1000) & = & g \\ k & = & \frac{g}{1000} \end{matrix}$ 
 k = 0.001

Hypothetically...

l = 1

 $v = \frac{4}{l}$ 
 v = 4

Solving for M:

 $\begin{matrix} 1000 & = & \frac{M}{l} \\ \frac{M}{l} & = & 1000 \\ M \frac{1}{l} & = & 1000 \\ M & = & 1000 l \end{matrix}$ 
 M = 1,000

 $d = \frac{M}{g}$ 
 d = 1,000

Solving for a:

 $\begin{matrix} d & = & \frac{a}{v} \\ \frac{a}{v} & = & d \\ a \frac{1}{v} & = & d \\ a & = & d v \end{matrix}$ 
 a = 4,000

 $p = \frac{d g}{M}$ 
 p = 1

 $h = S a$ 
 h = 16,720,000

16.72 (or 418 / 25, or 16 & 18 / 25) is THE HEAT CAPACITY IN [KJ].